고정 헤더 영역
상세 컨텐츠
본문
Abaqus/Explicit는 접촉 상호 작용을 만들기 위해 두 가지 알고리즘을 제공한다. 일반(자동) 접촉 알고리즘은 사용되는 표면 종류에 거의 제한이 없으며, 접촉을 매우 쉽게 정의할 수 있다. 접촉 쌍 알고리즘은 가끔 사용하는 표면의 종류에 더 많은 제약이 있으므로 더욱 신중하게 접촉을 정의해야 한다. 하지만 이 알고리즘을 사용하면 현재 일반 접촉 알고리즘에서 지원할 수 없는 몇 가지 상호 작용 특성을 다룰 수 있다. 일반 접촉 상호 작용은 일반적으로 모델의 모든 객체를 포함하여 Abaqus/Explicit가 자동으로 정의하는 기본 요소 서피스에 자체 접촉을 지정하여 정의한다. 접촉 영역을 좁히기 위해 특정 표면 쌍을 포함하거나 제거할 수 있다. 접촉 쌍 상호 작용은 상호 작용하는 접촉 쌍을 개별적으로 지정함으로써 정의된다.
Abaqus/Explicit 접촉의 공식은 구속을 계산하는 방법, 접촉면을 가중하는 방법과 미끄럼 공식을 포함한다.
Abaqus/Explicit의 일반적인 접촉은 표면에 대한 절점의 침투와 가장자리의 침투를 현재 배치에서 탐색하고, 접촉의 제약은 페널티 방법을 사용하여 수행한다. 접촉력을 침투 거리와 연관시키는 페널티 강성은 시간 증분에 미치는 영향을 최소화하고 침투량을 무시할 수 있도록 Abaqus/Explicit가 자동으로 선택한다.
접촉 쌍 알고리즘은 예측자/수정자 방법을 사용하여 접촉 조건을 정확하게 준수하는 운동학적 접촉의 공식을 기본적으로 사용한다. 첫 번째 증분은 접촉이 일어나지 않는다고 가정하여 계산한다. 증분이 끝날 때 침투가 있으면 접촉 구속이 작용하는 올바른 배치를 얻어지도록 가속도를 수정한다.
접촉 쌍에 대한 법선 방향의 접촉 구속은 필요한 경우 페널티 접촉 방법에 따라 제공될 수 있다. 이것은 운동학적 방법으로는 불가능한 몇 가지 접촉 종류를 만들 수 있다. 예를 들어, 페널티 방법을 사용하면 두 강체 표면 사이의 접촉을 만들 수 있다(양쪽 표면이 해석용 강체 표면인 경우 제외). 페널티 방법에 따라 접촉 공식을 사용하면, 페널티 강성에 침투 거리를 곱한 값과 같은 접촉력이 침투 위치에서 Master 절점과 Slave 절점에 각각 반대 방향으로 작용한다. 페널티 강성은 Abaqus/Explicit에서 자동으로 선택하며 일반 접촉 알고리즘에서 사용하는 것과 유사하다. 서로 다른 표면 사이의 접촉 상호 작용에 대한 페널티 강성은 페널티 배율 또는 ‘매끄러운’ 접촉 관계를 지정하여 변경할 수 있다.
순수한 Master/Slave 방법을 사용하면 한쪽 표면이 Master 표면에, 나머지는 Slave 표면이다. 두 물체가 접촉하면 침투가 감지되고, 구속 계산 방법(운동학 또는 페널티)에 따라 접촉 구속이 적용된다. 순수한 Master/Slave 가중치는 (구속을 계산하는 방법과 관계없이) Master 서피스에 Slave 절점을 침투하는 것에 저항한다. 다음 그림과 같이 Slave 서피스의 요소망이 아주 미세하지 않으면 Slave 서피스에 대한 Master 절점의 침투가 감지되지 않을 수 있다.
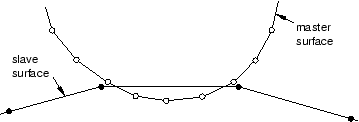
균형 잡힌 Master/Slave의 접촉은 순수한 Master/Slave 방법을 두 번 적용하고, 두 번째의 경우 Master와 Slave의 역할을 반전시킨다. 첫 번째 접촉 구속에서 서피스 1은 Slave가 되고, 두 번째 구속에서 서피스 2가 Slave가 된다. 운동학적으로 균형 잡힌 Master/Slave 접촉에서 두 번째 수정은 나머지 모든 침투를 제거하는 데 필요하다. 운동학적 방법을 사용한 균형 잡힌 Master/Slave의 접촉 제한은 다음 그림에 나와 있다.
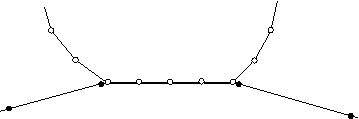
균형 잡힌 방법은 접촉하는 물체 사이의 침투를 최소화하고 결과적으로 대부분 문제에서 더 정확한 결과를 제공한다.
일반 접촉 알고리즘은 가능한 한 균형 잡힌 Master/Slave 가중 방법을 사용한다. 그러나 항상 순수한 Slave 표면이 되는 절점 서피스를 사용하는 경우 순수한 Master/Slave 가중 방법을 사용한다. 접촉 쌍 알고리즘에서 주어진 접촉 쌍에 어떤 종류의 가중 방법을 사용할지는 사용되는 두 개 서피스의 특성과 사용된 구속조건을 계산하는 방법에 따라 결정된다.
서로 다른 표면 사이의 접촉 상호 작용을 정의할 때 상대 미끄럼 양이 미세한지 또는 유한한지 결정해야 한다. 기본값(일반 접촉 상호 작용의 경우 유일한 옵션)은 더 일반적인 유한 미끄럼 공식이다. 두 표면 사이의 상대 운동이 요소 표면의 특성 길이에 비해 약간의 양일 때 미세 미끄럼 공식을 사용하는 것이 좋다. 적용할 수 있는 경우 미세 미끄럼 공식을 사용하면 분석이 효율적이다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 예제: 회로 기판 낙하 시험 (1) | 2024.06.09 |
|---|---|
| [Abaqus] Abaqus/Explicit에서 모델링 고려 사항 (0) | 2024.06.06 |
| [Abaqus] 예제: 랩 조인트의 전단 (1) | 2024.06.06 |
| [Abaqus] 예제: 채널 성형 해석 (0) | 2024.06.06 |
| [Abaqus] Abaqus/Standard에서 강성 표면 모델링의 주의 사항 (0) | 2024.06.05 |





