고정 헤더 영역
상세 컨텐츠
본문
선형 소변형(小變形) 해석 단계는 Abaqus/Standard에서만 사용할 수 있다. 선형 증분 단계의 출발점을 모델의 기준 상태라고 한다. 선형 증분 단계를 해석의 첫 번째 단계에서 사용하면 초기 조건을 사용하여 지정된 모델의 상태가 기준 상태가 된다. 그렇지 않으면 기준 상태는 선형 소변형 단계 직전의 일반 단계가 끝날 때 해석 상태이다. 증분 단계의 구조물 반응은 정의에 따라 선형이지만 이전 일반 단계에서 모델의 응답은 비선형일 수 있다. 이전 일반 단계에서 모델에 비선형 응답이 있는 경우 Abaqus/Standard는 증분 절차의 선형 강성으로 현재 탄성률을 사용한다. 다음 그림에서 이 탄성률은 탄성 재료의 초기 탄성률, 초탄성 재료의 경우 탄젠트 탄성률이다.
* Perturbation은 시스템에 영향을 주긴 하지만, 아주 크게 바꾸는 건 아닌 것을 의미한다.
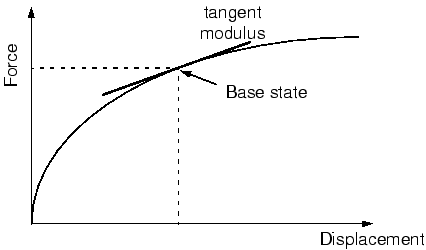
증분 단계에서 하중은 모델의 응답이 접선 탄성률로 예측된 응답에서 크게 벗어나지 않을 정도로 작아야 한다. 해석에 접촉이 포함되면 표면 사이의 접촉 상태는 증분 단계에서 변하지 않는다. 기준 상태에서 닫힌 지점은 닫힌 상태이고 열린 지점은 열린 상태이다.
1) 선형 증분 단계에서 시간
증분 단계 후에 다른 일반 단계가 계속되면 일반 단계는 Abaqus/Standard의 출발점으로서 증분 단계가 종료할 때의 모델 상태가 아니고, 직전의 일반 단계의 종료할 때의 모델의 상태를 사용한다. 선형 증분 단계에서 응답은 해석에 영구적인 영향을 미치지 않는다. 따라서 Abaqus/Standard는 선형 증분 단계의 단계 시간을 해석의 전체 시간에 포함하지 않는다. 실제로 Abaqus/Standard는 증분 단계의 단계 시간을 매우 작게(10-36) 정의하여 전체 시간에 시간을 더해도 영향을 미치지 않는다. 이 규칙의 예외는 모드 동적 절차가 있다.
2) 선형 증분 단계에서 하중 지정
선형 증분 단계에서 제공하는 하중과 규정된 경계 조건은 항상 단계의 로컬이다. 선형 증분 단계에서 주어진 하중의 크기(규정 경계 조건의 크기 포함)는 항상 하중의 증분이며, 전체 값은 아니다. 마찬가지로 해법 변수의 출력은 기준 상태의 변수를 포함하지 않는 증분 값이다.
일반적인 단계와 증분 단계가 혼합된 간단한 하중 이력의 예로 다음 그림에 표시된 활과 화살표를 고려한다.
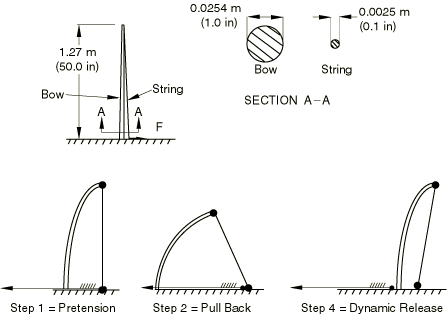
1단계는 활을 끈으로 묶는다. 활의 현에 초기 인장력을 작용한다. 2단계는 화살로 현을 뒤로 당긴다. 결과적으로 현에 변형률 에너지가 추가로 저장된다. 3단계는 선형 소변형 해석 단계이며, 하중이 주어진 시스템의 고유 진동수를 조사하는 고유치 진동 해석을 수행한다. 이런 단계는 단계 1과 2 사이에 삽입되어 현에 초기 인장력이 작용한 직후에 현이 뒤로 당기기 전에 활과 현의 고유 진동수를 결정할 수 있다. 4단계는 비선형 동역학 해석이다. 이 단계에서 활의 현을 해방하고, 그에 따라, 2단계에서 활의 현을 뒤로 당기는 것으로, 이 현에 축적된 변형률 에너지가 운동 에너지로 화살에 주어지고, 화살이 활로부터 풀린다. 이 단계는 활의 비선형 응답을 발전시키고 동적 효과를 고려한다.
이 예제에서 각 비선형 일반 해석 단계는 이전의 비선형 일반 해석 단계가 끝날 때의 상태를 초기 조건으로 사용한다는 것이 분명하다. 예를 들어, 이 이력의 동적 응답 부분에는 하중이 없다. 이 동적 응답은 정적 단계에서 축적된 변형률 에너지 일부가 해제되면서 발생한다. 이 효과는 모델에 자연스러운 순서 종속성을 도입한다. 비선형 일반 해석 단계는 그들이 정의하는 현상의 발생 순서로 정의된다. 선형 소변형 해석 단계는 이 순서에서 적절한 시간에 삽입되고 그 시간에 시스템의 선형 거동을 조사한다.
더 복잡한 하중 이력은 다음 그림 같다. 이 그림은 스테인리스강 싱크대의 제조와 사용 단계를 보여주는 개략도이다. 이 싱크대는 펀치, 다이, 블랭크 홀더를 사용하여 강판으로 성형한다. 이 성형 해석은 여러 일반 단계로 구성된다. 일반적으로 첫 번째 단계는 블랭크 홀더 압력을 적용하고 두 번째 단계에서 펀치로 성형을 해석한다. 세 번째 단계는 공구를 제거하고 싱크대를 스프링백 하여 최종 모양을 찾는다. 이 단계는 연속적인 하중 이력을 만들기 때문에 모두 일반 단계이며, 각 단계의 시작 상태는 이전 단계의 종료 상태이다. 이런 단계에는 분명히 여러 비선형 효과(소성, 접촉, 대변형)가 포함된다. 세 번째 단계가 끝나면 싱크대는 성형 가공으로 잔류 응력과 비탄성 변형이 있다. 또한 싱크대의 두께는 이 제조 공정의 직접 결과로 변경된다.
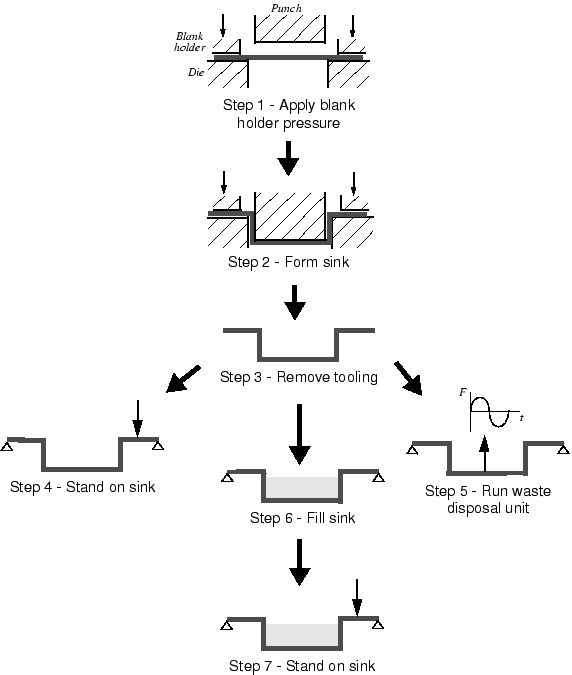
그다음 싱크대를 설치한다. 조리대에 부착된 싱크대의 가장자리 주위에 경계 조건을 적용한다. 여러 다른 하중 조건에 대한 싱크대 응답에 주목할 수 있으며, 이 경우 응답을 해석해야 한다. 예를 들어, 싱크대에 사람이 서 있으면 싱크대가 손상되지 않도록 해석해야 한다. 따라서 4단계는 국부 압력 하중에 대한 싱크대의 정적 응답을 해석하는 선형 증분 단계이다. 4단계의 결과는 성형 가공 후 싱크대의 상태에서 증분이 될 것을 상기시켜야 한다. 싱크대는 성형 해석의 시작에서 볼 때 그보다 훨씬 변형되었다는 것을 알 수 있다. 이 가정에서 2mm의 처짐은 성형 후(3단계가 끝난 후) 싱크대의 최종 모양에서 사람의 무게로 생긴 추가 처짐이다. 모든 처짐은 변형 전 플레이트의 형상으로부터 측정되며, 이 2mm와 3단계의 끝에서 처짐의 합이다.
이 싱크대는 폐기물 처리 장치가 설치될 수 있다. 따라서 특정 주파수의 조화 하중에 대한 정상 동적 응답을 해석해야 한다. 따라서 5단계는 직접 정상 동적 절차를 사용하는 두 번째 선형 증분 단계이며, 폐기물 처리 장치가 설치된 위치에 하중을 적용한다. 이 단계의 기준 상태는 직전의 일반 단계가 종료할 때 성형 가공(3단계)의 종료할 때의 상태이다. 이전 증분 단계(4단계)에서 응답은 무시한다. 따라서 이 두 가지 증분 단계는 모델의 기준 상태에 주어진 하중에 대한 싱크대 응답과 별도의 독립적인 해석이다.
또한 일반 단계가 이 해석에 포함되면, 단계가 시작할 때 구조의 상태는 이전 일반 단계(3단계)가 끝날 때의 상태이다. 따라서 6단계는 일반 단계이며, 물이 채워진 싱크대를 만드는 하중을 줄 수 있다. 이 단계에서 응답은 선형 또는 비선형일 수 있다. 이 일반 단계 다음에 7단계에서 4단계에서 수행된 해석을 다시 해석할 수 있다. 그러나 이 경우 기준 상태(마지막 일반 단계의 끝에서 구조물의 상태)는 6단계의 끝에서 구조물의 상태이다. 따라서 이 응답은 빈 싱크대가 아닌 물로 채워진 싱크대의 응답이다. 다른 정상적인 동역학 해석을 하더라도 물의 질량(응답을 크게 변경)이 해석에서 고려되지 않기 때문에 결과가 부정확해진다.
Abaqus/Standard의 다음 절차는 항상 선형 증분 단계이다.
• 선형 좌굴 고유치 해석
• 고유 진동수의 추출
• 과도 모드 동적 응답 해석
• 불규칙 응답 해석
• 응답 스펙트럼 해석
• 정상 조화 동적 응답 해석
정적 절차는 일반 절차와 선형 증분 절차 중 하나일 수 있다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 예제: 진동 재해석 (2) | 2024.06.03 |
|---|---|
| [Abaqus] 예제: 배관계 진동해석 (0) | 2024.06.03 |
| [Abaqus] 다단계 해석 - 일반 해석 절차 (0) | 2024.06.02 |
| [Abaqus] Abaqus에서 하중의 의미 (0) | 2024.06.02 |
| [Abaqus] 체적 잠금을 줄이는 기술 (0) | 2024.06.01 |





