고정 헤더 영역
상세 컨텐츠
본문
Abaqus는 다양한 요소를 사용한다. 이 다양한 요소 라이브러리는 다양한 문제를 해결하는 강력한 도구를 제공한다. Abaqus/Explicit에서 사용하는 요소는 일부 예외를 제외하고 Abaqus/Standard에서 사용하는 요소에 모두 포함된다. 이 절은 요소의 거동에 영향을 미치는 요소의 다섯 가지 특징을 소개한다.
1) 요소 특성화
각 요소는 요소 종류, 요소 종류와 관련된 자유도, 절점 수, 공식화, 적분에 다음과 같은 특징이 있다. Abaqus의 각 요소는 T2D2, S4R 또는 C3D8I 같은 고유 이름이 있다. 요소 이름은 요소의 다섯 가지 측면을 각각 식별한다. 요소 이름 규칙은 이 장에서 설명한다.
다음 그림은 응력 해석에서 가장 많이 사용하는 요소이다. 서로 다른 요소의 주요 차이점 중 하나는 각 요소가 가정하는 기하 형상이다. 다른 장에서 연속체 요소, Shell 요소, Truss 요소, 강체 요소)를 자세히 설명한다. 이 책에서 다른 요소는 다루지 않는다.
요소 이름의 첫 글자는 요소의 종류를 나타낸다. 예를 들어, S4R의 S는 Shell 요소를 나타내고, C3D8I의 C는 연속체(Continuum) 요소를 나타낸다.
자유도(degree of freedom)는 해석하는 동안 계산되는 기본 변수이다. 응력/변위 해석에서 자유도는 각 절점의 이동 자유도이다. Beam 요소나 Shell 요소와 같은 일부 요소는 회전 자유도도 가지고 있다. 열전달 해석의 자유도는 각 절점의 온도이다. 따라서 자유도가 응력 해석과 다르므로 열전달 해석은 응력 해석과 다른 요소를 사용해야 한다.

Abaqus는 다음과 같이 번호 규칙을 자유도에 사용한다. 1, 2, 3방향은 절점에서 로컬 좌표계를 정의하지 않으면 각각 글로벌 1, 2, 3방향에 해당한다.
| 1 | 1 방향 이동 |
| 2 | 2 방향 이동 |
| 3 | 3 방향 이동 |
| 4 | 1축 기준 회전 |
| 5 | 2축 기준 회전 |
| 6 | 3축 기준 회전 |
| 7 | 단면 보 요소의 뒤틀림 |
| 8 | 음압, 틈새 압력 또는 정수 유체 압력 |
| 9 | 전위 |
| 10 | 커넥터 재료 흐름(길이 단위) |
| 11 | 연속체 요소의 온도(또는 질량 확산 해석의 정규화된 농도) 또는 Beam과 Shell의 두께를 통한 첫 번째 지점의 온도 |
| 12+ | Beam과 Shell의 두께를 통한 다른 지점의 온도 |
축대칭 요소는 예외이며, 변위와 회전 자유도는 다음과 같다. r-방향(반경 방향)과 z-방향(축 방향)은 절점에서 로컬 좌표계를 정의하지 않으면 각각 글로벌 1과 2방향이다.
| 1 | r 방향으로 이동 |
| 2 | z 방향으로 이동 |
| 6 | rz 평면에서 회전 |
여기서 구조 문제만 다루므로, 이동과 회전 자유도가 있는 요소만 다룬다. 기본적으로 Abaqus/CAE는 알파벳 x-y-z를 뷰 방향 좌표축에 사용한다. 이 책은 자유도와 축 제목이 일치하도록 숫자 1-2-3을 사용한다.
이전 장에서 설명한 변위, 회전, 온도 등의 자유도는 요소의 절점 위치에서만 계산된다. 요소 안의 임의의 다른 점의 변위는 절점 변위로부터 보간(補間)하여 결정한다. 그림과 같이 보통 보간 함수의 차수는 요소에 사용하는 절점 수에 따라 다르다.

- 8절점 6면체 요소와 같이 모서리에만 절점이 있는 요소는 각 방향에서 선형 보간법을 사용한다. 따라서 이런 요소를 선형 요소 또는 1차 요소라고 한다.
- 20절점 6면체 요소와 같이 중간에 절점이 있는 요소는 2차 보간 함수를 사용한다. 따라서 이런 요소를 2차 요소라고 한다.
- 10절점 4면체 요소와 같이 중간 절점이 있는 수정 삼각형 요소 또는 수정 4면체 요소는 수정된 2차 보간 함수를 사용한다. 따라서 이런 요소를 수정 요소 또는 수정 2차 요소라고 한다.
Abaqus/Standard는 선형 요소와 2차 요소를 모두 제공한다. Abaqus/Explicit는 선형 요소만 제공하며, 예외로 2차 요소, 수정 4면체 요소와 수정 3각형 요소를 제공한다.
보통 요소의 절점 수는 요소의 이름으로 구별한다. 8절점 6면체 요소는 C3D8, 8절점 일반 Shell 요소는 S8R이다. 요소 종류는 약간 다른 규칙이 사용되며, 요소 이름은 보간 함수의 차수로 결정한다. 예를 들면, 1차 3차원 Beam 요소는 B31이며, 2차 3차원 Beam 요소는 B32이다. 축대칭 Shell 요소와 축대칭 Membrane 요소도 유사한 규칙을 사용한다.
요소의 공식화(Formulation)는 요소의 거동을 정의하는 데 사용하는 수학적 이론을 의미한다. 적응형 요소망을 사용하지 않으면 Abaqus의 모든 응력/변위 요소는 Lagrange 또는 재료 모델을 바탕으로 한다. 바꿔 말하면, 요소와 관련된 재료는 전체 해석을 진행하는 동안 요소와 연관되어 있으며, 재료는 요소 경계를 넘어서 흐를 수 없다. Lagrange와 다른 Euler 거동에서 요소는 공간에 고정되어 재료가 요소를 통해 흐른다. Euler 거동은 유체 역학 해석에 자주 사용된다. Abaqus/Standard는 대류 열전달을 해석할 때 Euler 요소를 사용한다. 적응형 요소망은 순수한 Lagrange 해석과 Euler 해석의 기능을 결합하여 요소의 운동을 재료와 독립적으로 만들 수 있다. Euler 요소와 적응형 요소망은 이 책에서 다루지 않는다.
다양한 종류의 거동을 해석하려고 Abaqus의 일부 요소는 서로 다른 공식화 요소를 포함한다. 예를 들어, Shell 요소는 일반 해석에 사용할 수 있는 Shell 요소, 박판(薄板)에 적합한 Shell 요소, 후판(厚板)에 적합한 Shell 요소의 세 가지 종류가 있다.
일부 Abaqus/Standard 요소는 표준 공식화와 그에 대한 몇 가지 공식화가 있다. 비표준 공식을 사용하는 요소는 요소 이름의 끝에 문자를 추가한다. 예를 들어, 연속체 요소, Solid 요소, 트러스 요소는 압력(연속체 요소) 또는 축력(Solid 요소와 트러스 요소)이 추가 미지수로 취급되는 하이브리드 요소가 있다. 이 요소는 이름 끝에 문자 ‘H’를 추가한다(C3D8H 또는 B31H).
일부 요소 공식화는 물리학 연계 문제를 해석할 수 있다. 예를 들어, 이름의 처음이 C이고 마지막이 T인 요소(예: C3D8T)는 기계적 자유도와 열적 자유도를 모두 가지며, 열응력 연계 해석에 사용하기 위한 것이다. 이 책에서는 가장 자주 사용하는 요소 공식화의 일부를 나중에 설명한다. Abaqus는 수치 기법을 사용하여 각 요소의 부피에 걸쳐 다양한 양을 적분한다. Abaqus는 대부분 요소에 가우스(Gauss) 적분을 사용하여 각 적분점의 재료 응답을 평가한다. Abaqus의 일부 요소는 완전 적분 또는 저감 적분을 사용할 수 있다. 이 선택은 문제에 따라 요소의 정확성에 크게 영향을 줄 수 있다. Abaqus는 요소 이름 끝에 문자 ‘R’을 사용하여 저감 적분 요소를 구별한다(단, 동시에 하이브리드 요소일 수도 있다. 이 경우 요소 이름의 끝은 문자열 ‘RH’이다. 예를 들어, CAX4는 4 절점, 완전 적분, 선형, 축대칭 Solid 요소이다. 그리고 CAX4R은 같은 요소의 저감 적분 요소이다. Abaqus/Standard는 완전 적분 요소와 저감 적분 요소를 모두 제공하지만, Abaqus/Explicit는 수정 4면체 요소, 수정 3각형 요소, 완전 적분 1차 Shell 요소, 완전 적분 1차 막 요소와 완전 적분 1차 6면체 요소를 제외하고 저감 적분 요소만 제공한다.
2) 연속체 요소
다양한 요소 중에서 연속체 요소는 기하 형상을 만드는 데 가장 폭넓게 사용한다. 개념적으로, 연속체 요소는 단순히 구성 요소의 재료를 구현하는 작은 부분을 만든다. 이런 요소는 서로 어떤 면이 결합하므로, 연속체 요소를 건물의 벽돌이나 모자이크 타일처럼 사용하여, 거의 모든 다양한 형태의 모델을 만들고, 거의 모든 종류의 하중을 줄 수 있다. Abaqus는 응력/변위 요소, 비구조(非構造) 요소와 다중 물리 연속체 요소를 제공한다. 이 책에서는 응력/변위 요소만 다룬다. Abaqus의 응력/변위 연속체 요소는 이름의 머리글자가 C이다. 그다음 두 문자는 요소의 차원과 예외도 있지만 대부분 유효한 자유도를 나타낸다. 문자열 3D는 3차원 요소, AX는 축대칭 요소, PE는 평면 변형률 요소, PS는 평면 응력 요소이다. 3차원 연속체 요소는 6면체, 5면체, 4면체일 수 있다. 가능하면 Abaqus는 6면체 요소 또는 2차 4면체 요소를 사용한다. 1차 4면체 요소(C3D4)는 일정 변형률(constant-strain)을 공식화하며, 정확한 솔루션을 얻으려면 매우 미세한 요소망이 필요하다. Abaqus는 면외 방향의 거동이 서로 다른 여러 종류의 2차원 연속체 요소를 제공한다. 2차원 요소는 4각형 또는 3각형일 수 있다. 다음 그림은 자주 사용되는 세 가지 종류이다.

평면 변형률 요소는 면외 변형률인 $ \varepsilon_{33} $을 ‘0’으로 가정한다. 이 요소를 사용하여 두꺼운 구조물을 해석할 수 있다. 평면 응력 요소는 면외 응력인 $ \sigma_{33} $을 ‘0’으로 가정한다. 이 요소를 사용하여 얇은 구조물을 해석할 수 있다. 비틀림이 없는 축대칭 요소(CAX계 요소)는 360°의 링 형태의 구조물을 해석할 수 있다. 이것은 축대칭 하중을 받는 축대칭 구조를 해석하는 데 적합하다.
또한 Abaqus/Standard는 일반화된 평면 변형률 요소, 비틀림을 포함하는 축대칭 요소와 축대칭 변형을 포함하는 축대칭 요소를 제공한다.
- 일반화된 평면 변형률 요소에서, 면외 변형은 모델 평면의 위치에서 선형으로 변화하는 일반화가 추가된다. 이 공식화는 두꺼운 단면의 열응력 해석에 적합하다.
- 비틀림을 포함하는 축대칭 요소는 대칭축을 중심으로 비틀 수 있는 축대칭 형상의 초기 모양을 만들 수 있다. 이런 요소는 축대칭 고무 부싱과 같은 원통형 구조의 비틀림을 해석할 때 유용하다.
- 축대칭 변형을 포함하는 축대칭 요소는 보통 휨(bending)의 결과로 발생하는 축대칭으로 변형할 수 있는 축대칭 형상의 초기 모양을 만들 수 있다. 이것은 전단 하중을 받는 축대칭 고무 마운트와 같은 문제를 해석할 때 유용하다.
2차원 Solid 요소는 다음 그림과 같이 절점의 순서가 요소의 반시계 방향이 되도록 1-2 평면에 정의해야 한다.
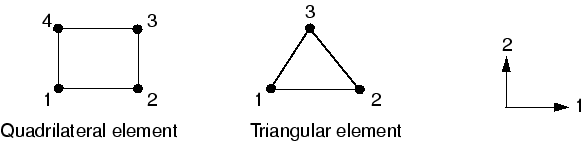
전처리기를 사용하여 요소망을 만들 때 모든 요소의 법선이 글로벌 3축의 양의 방향과 같은 방향을 향하도록 해야 한다. 요소의 절점이 올바른 순서로 정의되지 않으면, 요소가 음수의 영역을 향하고 있다는 것을 나타내는 오류 메시지가 Abaqus에서 출력된다.
모든 응력/변위 연속체 요소는 각 절점에 이동 자유도를 가진다. 따라서 3차원 요소는 자유도 1, 2, 3이 유효하고, 평면 변형률 요소, 평면 응력 요소와 비틀림이 없는 축대칭 요소는 자유도 1과 2만 유효하다.
모든 Solid 요소는 요소와 관련된 재료와 추가 형상 정보를 정의하는 Solid 요소 특성을 참조해야 한다. 3차원과 축대칭 요소는 요소 형상을 절점 좌표로 완벽히 정의할 수 있으므로 추가 형상 정보가 필요하지 않다. 평면 응력 요소와 평면 변형률 요소는 요소의 두께를 지정한다. 지정하지 않으면 기본값 1을 사용한다.
Abaqus/Standard의 연속체 요소에서 사용할 수 있는 다른 공식화에는 부적합 모드(incompatible mode) 공식화(요소 이름의 끝 또는 끝에서 두 번째 문자 I)와 하이브리드(hybrid) 요소 공식화(요소 이름의 마지막 문자 H)가 있으며, 이 책에서 자세히 설명한다.
Abaqus/Standard는 4각형과 6면체 요소에 완전 적분이나 저감 적분을 선택할 수 있다. Abaqus/Explicit는 6면체 요소에 완전 적분이나 저감 적분을 선택할 수 있다. 하지만 4각형 1차 요소는 저감 적분만 사용할 수 있다. 공식화와 적분 종류는 Solid 요소의 정확성에 상당한 영향을 미친다.
기본적으로 응력과 변형률 같은 요소 출력 변수는 글로벌 직교 좌표계를 참조한다. 따라서 그림 3.5(a)에 표시된 적분점에서 응력 성분은 글로벌 1방향으로 작용한다. 그림 3.5(b)와 같이 대변형 해석 중에 요소가 회전하더라도 기본값은 변하지 않고, 요소 변수를 정의하는 기초 데이터로 글로벌 직교 좌표계를 사용한다.
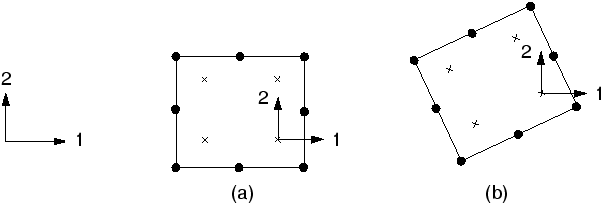
그러나 Abaqus에서 요소 변수에 로컬 좌표계를 정의할 수 있다. 이 로컬 좌표계는 대변형 해석에서 요소의 움직임과 함께 회전한다. 로컬 좌표계는 물체가 복합 재료의 섬유 방향과 같은 고유한 재료 방향을 가질 때 매우 유용하다.
3) Shell 요소
Shell 요소는 하나의 치수(두께)가 다른 치수보다 훨씬 작고, 두께 방향의 응력이 무시할 정도로 작은 구조물에 사용한다. Abaqus Shell 요소의 이름은 S로 시작한다. 축대칭 Shell 요소의 이름은 모두 문자열 SAX로 시작한다. Abaqus/Standard는 또한 축대칭 변형을 포함하는 축대칭 Shell을 제공하며, 이들은 문자열 SAXA로 시작한다. Shell 요소 이름의 첫 번째 숫자는 요소의 절점 수이다. 하지만 축대칭 Shell은 예외이며, 첫 번째 숫자는 보간법 차수이다. Abaqus는 일반 Shell 요소와 연속체 Shell 요소는 2종류의 Shell 요소가 있다. 일반 Shell 요소는 요소 평면의 치수, 그 면의 법선 방향과 초기 곡률을 정의한 다음, 참조 평면을 이산화한다. 대조적으로 연속체 Shell 요소는 3차원 Solid 요소와 유사하지만 완전한 3차원 물체를 이산화하는 점에서 운동학 거동과 구성 거동은 일반 Shell 요소와 같이 공식화된다. 이 책은 일반 Shell 요소만 설명하므로 이 요소를 단순히 Shell 요소라고 한다. Abaqus/Standard는 일반 3차원 Shell 요소를 범용, 박판 전용, 후판 전용의 3가지 형식으로 사용할 수 있다. 범용 Shell과 축대칭 변형이 포함된 축대칭 Shell은 유한 Membrane 변형과 임의 대회전을 포함한다. 박판 전용, 후판 전용인 3차원 Shell 요소는 미소한 변형에서만 임의 대회전을 포함한다. 범용 Shell은 Shell의 두께가 요소의 변형으로 변화할 수 없다고 가정한다. 선형과 2차 보간 함수를 사용하여 3각형과 4각형 요소를 사용할 수 있다. 선형과 2차 축대칭 Shell 요소를 사용할 수 있다. 모든 4각형 Shell 요소(단, S4 제외)와 3각형 Shell 요소 S3/S3R은 저감 적분을 사용한다. S4 요소와 다른 삼각형 Shell 요소는 완전 적분을 사용한다.
다음 표는 Abaqus/Standard에서 사용할 수 있는 Shell 요소를 요약한 것이다.
Abaqus/Standard의 세 가지 종류의 Shell 요소
| 범용 Shell | 박판 전용 Shell | 후판 전용 Shell |
| S4, S4R, S3/S3R, SAX1, SAX2, SAX2T, SC6R, SC8R | STRI3, STRI65, S4R5, S8R5, S9R5, SAXA |
S8R, S8RT |
Abaqus/Explicit의 모든 Shell 요소는 범용이다. 유한 Membrane 변형률과 미소 막 변형률의 공식화를 사용할 수 있다. 선형 보간 함수로 3각형과 4각형 요소를 사용할 수 있다. 또한 선형 축대칭 Shell 요소를 사용할 수 있다.
다음 표는 Abaqus/Explicit에서 사용할 수 있는 Shell 요소를 요약한 것이다.
Abaqus/Explicit의 두 가지 종류의 Shell 요소
| 유한 변형 Shell | 미세 변형 Shell |
| S4, S4R, S3/S3R, SAX1 | S4RS, S4RSW, S3RS |
대부분의 Explicit 해석은 대변형률 Shell 요소가 적합하다. 그러나 해석에 미세 Membrane 변형률과 임의 대회전을 포함한 소변형률 Shell 요소는 계산 효율이 높다. S4RS 요소와 S3RS 요소는 뒤틀림(Warping)을 고려하지 않지만 S4RSW 요소는 고려한다. 이름이 숫자의 5로 끝나는 Abaqus/Standard의 3차원 요소(S4R5, STRI65 등)는 절점마다 3개의 이동과 2개의 면내 회전(Shell의 법선 방향 주위의 회전은 없다)으로부터 5가지 자유도가 있다. 그러나 필요할 때 6개의 자유도가 절점에서 활성화된다. 예를 들어 회전 경계 조건을 적용하거나 절점이 Shell의 선에 있을 때 활성화된다. 다른 3차원 Shell 요소는 절점당 6개의 자유도를 가진다(3개의 이동과 3개의 회전). 축대칭 Shell은 절점당 3개의 자유도를 가진다.
| 1 | r 방향으로 이동 |
| 2 | z 방향으로 이동 |
| 6 | rz 평면에서 회 |
모든 Shell 요소는 요소와 관련된 두께와 재료 특성을 정의하는 Shell 요소 특성을 입력해야 한다. Shell 단면의 강성은 해석을 시작할 때 한 번 또는 해석 중에 계산할 수 있다. 단면 강성을 해석 중에 계산하려면 Abaqus는 수치 적분을 사용하여 Shell 두께 방향의 선택된 지점에서 거동을 계산한다. 그림 3.6에 표시된 이런 점을 단면점(section point)이라고 한다. 관련 재료 특성은 선형이나 비선형일 수 있다. Shell 두께 방향의 단면점은 임의의 홀수로 지정할 수 있다.

단면 강성으로 해석을 시작할 때 한 번만 계산하도록 선택하면 단면 거동을 정의하여 선형 또는 비선형 거동을 해석할 수 있다. 이 경우 Abaqus는 Shell의 단면 거동을 단면의 물리량(면적, 단면 2차 모멘트 등)으로 직접 만들기 때문에 요소의 단면에 걸쳐 물리량을 적분할 필요가 없다. 따라서 이 옵션은 계산량이 적다. 단면 응답은 힘과 모멘트로 계산한다. 응력과 변형률은 출력이 필요한 경우만 계산한다. 이 방법은 Shell 응답이 선형 탄성이면 사용하는 것이 좋다. Shell의 요소 출력 변수는 각 Shell 요소의 표면에 존재하는 로컬 재료 방향으로 정의한다. 모든 대변형 해석에서 이런 축은 요소의 변형과 함께 회전한다. 또한 대변형 해석에서 요소의 변형과 함께 회전하는 로컬 재료 좌표계를 정의할 수 있다.
4) Beam 요소
Beam 요소는 한 치수(길이)가 다른 두 치수보다 상당히 크고, Beam 축을 따르는 방향의 응력만 중요하다. Abaqus에서 Beam 요소의 이름은 첫 글자가 B이다. 다음 문자는 요소의 차원을 나타낸다. 2차원 Beam은 2, 3차원 Beam은 3이다. 세 번째 문자는 사용되는 보간 함수를 나타낸다. 선형 보간 함수는 1, 2차 보간 함수는 2, 3차 보간 함수는 3이다. 선형, 2차와 3차 Beam은 2차원과 3차원에서 사용할 수 있다. 3차 Solid는 Abaqus/Explicit에서 사용할 수 없다. 3차원 Beam은 각 절점에 3개의 이동 자유도(1~3)와 3개의 회전 자유도(4~6)로 구성된 6개의 자유도를 가진다. ‘개방 단면’ 종류의 Beam(예: B31OS)은 Abaqus/Standard에서 사용할 수 있으며, Beam 단면의 뒤틀림(Warping)을 나타내는 추가 자유도(7)를 가진다. 2차원 Beam은 각 절점에 2개의 이동 자유도(1과 2)와 모델 평면의 수직 방향을 축으로 하는 하나의 회전 자유도(6)로 구성된 3개의 자유도를 가진다. 모든 Beam 요소는 요소와 관련된 재료와 Beam 단면 형상(요소의 단면 형상)을 정의하는 Beam 요소 특성을 입력해야 한다. 절점 좌표는 단면의 길이만 정의한다. 단면은 모양과 치수를 지정하여 기하 형상을 정의할 수 있다. 또 다른 방법은 단면의 공학 특성(면적, 단면 2차 모멘트 등)을 지정하여 일반 단면 형상을 정의하는 것이다. Beam 단면 형상을 기하 형상으로 정의하면, Abaqus는 Beam 단면 거동을 단면의 수치 적분으로 계산한다. 따라서 재료 모델은 선형이거나 비선형일 수 있다. 단면의 치수가 아닌 단면의 공학적 특성(면적, 단면 2차 모멘트, 비틀림 상수)을 제공하면 Abaqus는 각 양을 요소 단면으로 적분할 필요가 없다. 따라서, 이 옵션은 계산량이 적다. 이 방법은 재료 모델을 선형이나 비선형으로 해석할 수 있다. 응답은 힘과 모멘트를 계산하고, 응력과 변형률은 출력을 요청했을 때만 계산한다. Abaqus/Standard에서 선형 테이퍼 단면의 Beam을 정의할 수 있다. 선형 응답의 일반화 단면과 표준 라이브러리 단면이 지원된다. 선형 Beam(B21과 B31)과 2차 Beam(B22와 B32)은 전단 변형이 가능하며, 유한 축 변형률을 고려한다. 따라서 이 요소는 길고 굵은 Beam 모델링 모두에 적합하다. Abaqus/Standard의 3차 Beam 요소(B23과 B33)는 대변형과 대회전이 가능하지만 전단 변형을 고려하지 않고 미소 축 변형을 가정한다. 따라서 이 요소는 가느다란 Beam 모델링에 적합하다. Abaqus/Standard는 얇은 벽을 가진 개방 단면 모델링에 적합한 선형과 2차 Beam 요소의 향상된 버전(B31OS와 B32OS)을 제공한다. 이 요소는 개방 단면(I-Beam, U-단면 채널 등)의 비틀림(torsion)과 뒤틀림(warping) 효과를 제공한다. 또한, Abaqus/Standard는 매우 가느다란 부재(예: 해양 석유 설비의 구부러지기 쉬운 라이저(Riser))와 매우 강한 링크를 표현하는 데 사용하는 하이브리드 Beam 요소를 제공한다.
3차원 전단 변형이 가능한 Beam 요소의 응력 성분은 축 응력($ \sigma_{11} $)과 비틀림에 의한 전단 응력($ \sigma_{12} $)이다. 전단 응력은 얇은 벽 단면의 단면 벽을 중심으로 작용한다. 대응하는 변형률도 측정이 가능하다. 전단 변형이 가능한 Beam은 단면 가로 방향의 전단력 추정치도 제공한다. Abaqus/Standard의 3차 Beam은 축 방향 변수만 가지고 있다. 개방 단면 공간은 비틀림 전단 응력이 무시할 정도로 작아서 축 방향 변수만 출력한다. 모든 2차원 Beam은 축 응력과 축 변형률만 사용한다. 축력, 휨 모멘트 지렛대에 어떤 힘이 가해질 때 생기는 힘의 모멘트와 Beam 로컬 축 주위의 곡률이 필요할 수 있다.
5) Truss 요소
트러스 요소는 인장과 압축 하중만을 유지할 수 있는 막대이다. 이 요소는 휨에 저항하지 않는다. 따라서, 핀으로 결합한 프레임을 만들 수 있다. 또한, 트러스 요소는 케이블과 스트링(String)을 근사할 때 사용할 수 있다(예: 테니스 라켓 등). 또한 트러스는 다른 요소 안에서 보강재를 표현할 때 사용할 수 있다. 모든 트러스 요소의 이름은 첫 글자가 T이다. 다음 두 문자는 요소의 차원을 나타낸다. 2D 트러스의 경우 2D, 3D 트러스의 경우 3D. 마지막 문자는 요소의 절점 수를 나타낸다. 선형과 2차 트러스는 2차원과 3차원에서 사용할 수 있지만 Abaqus/Explicit에서는 2차 트러스를 사용할 수 없다. 트러스 요소는 각 절점에 이동 자유도 만을 가지며, 3차원 트러스 요소는 자유도 1, 2, 3을 가지며, 2차원 트러스 요소는 자유도 1과 2를 가진다. 모든 트러스 요소는 재료 특성을 요소와 연관시키고, 트러스 요소 특성에 요소의 단면적을 입력한다. 표준 공식화 외에도 Abaqus/Standard는 하이브리드 트러스 요소 공식화를 사용할 수 있다. 이것은 전체 구조의 강성보다 상당히 큰 강성을 갖는 매우 강한 링크를 만드는 데 유용하다. 트러스 요소는 축 응력과 축 변형률을 출력할 수 있다.
[Abaqus] 강체 요소란 무엇인가?
그림과 같이 Abaqus의 강체는 강체 기준 절점(rigid body reference node)이라는 하나의 절점으로 움직이는 절점과 요소 세트이다. 강체의 형상은 2차원 스케치를 회전하거나 압출하여 얻은 해석용 표면
sidedesk.tistory.com
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 예제: 캔틸레버 보 해석 (0) | 2024.04.08 |
|---|---|
| [Abaqus] 강체 요소란 무엇인가? (1) | 2024.04.08 |
| [Abaqus] 예제: 천장 호이스트 모델 만들기 (2) | 2024.04.07 |
| [Abaqus] 내연적과 외연적 절차의 비교 (1) | 2024.04.06 |
| [Abaqus] Abaqus 해석의 구성 요소 (0) | 2024.04.06 |




