로켓이 추력을 만드는 원리

로켓은 리프트오프를 한 뒤 스스로 탑재한 추진제를 소비하므로 자신의 질량을 감소시키면서 로켓의 기준 축 방향으로 비행한다. 이런 로켓의 운동은 어떻게 설명할 수 있을까?

 

이상 상태의 로켓 운동

Ref. Introduction to Rocket Propulsion | Physics (lumenlearning.com)

 

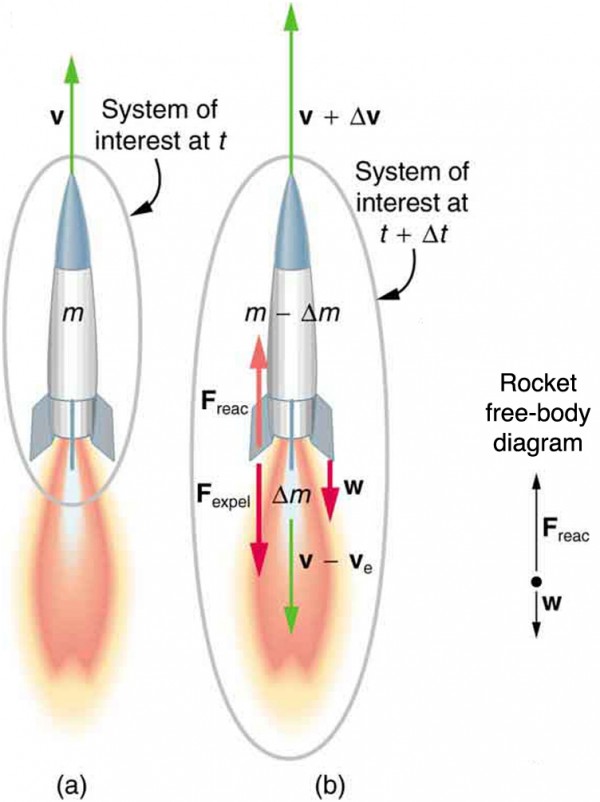
처음에 로켓이 비행하는 상황을 단순화하여, 중력(만유인력)과 공기가 없는 이상 상태를 생각해 보자. 이때 그림과 같이 로켓을 단일 시스템으로 생각하면 ‘시간 $t$에서의 상태’와 ‘미소 시간 $\Delta t$가 지난 상태 ($t+ \Delta t $)’에 ‘운동량 보존 법칙’이 적용된다. 다시 말하면, “질량이 일정한 로켓에서 일하는 외력이 ‘0’일 때 로켓의 운동량은 보존된다.”라는 고전역학의 법칙이 적용된다. 운동량 보존 법칙이 바로 ‘뉴턴의 운동 법칙’이다.

 

로켓의 운동을 ‘로켓 기체’와 ‘배출가스’라는 2가지 물체의 상호작용으로 분석하면, 이 로켓에 외력이 작용하지 않을 때 운동량은 보존된다. ‘운동량’은 ‘질량 × 속도’로 정의되는 물리량이다. 질량은 스칼라, 속도는 방향을 가진 벡터이므로 운동량은 벡터이다.

 

여기서 시간 $t$에서의 로켓 기체의 질량을 $m$, 관성 좌표계에서 속도를 $v$ , 미소 시간 간격 $\Delta t$ 사이에 로켓이 배출하는 추진제 질량을 $\Delta m$ , 연소가스의 배출 속도(로켓에 대한 상대 속도)를 $v_e$라고 하자. 또 $\Delta t$ 사이에 로켓은 속도가 증가하므로, 그 증가분을 $\Delta v$ 라고 하자. 보통 $v_e$는 일정하다.

 

이 시스템은 외력이 작용하지 않으므로 운동량 보존 법칙에 따라 시간 $t$와 $t+ \Delta t $에서 운동량은 변하지 않는다. 그러므로 다음 식이 성립할 것이다.

$$ mv = (m - \Delta m)(v + \Delta v) + \Delta m ( v - v_{e} ) $$

$$ \therefore m \cdot \Delta v = v_{e} \cdot \Delta m $$

여기서 $ \Delta m \times \Delta v $는 2차 미소량이므로 무시하면, 다음의 로켓 운동방정식을 얻을 수 있다.

$$ F = m {\Delta v \over \Delta t} = v_{e} {\Delta m \over \Delta t} $$

여기서 $v_e$는 연소가스의 배출 속도(로켓에 대한 상대 속도), $\delta m / \Delta t$는 연소가스의 단위 시간당 배출 질량이다.

 

로켓의 운동방정식은 로켓의 주위가 진공 상태일 때 성립한다. 실제 우주로켓은 지표에서 비행을 시작하므로 대기의 영향을 고려해야 한다. 그림과 같이 실제 환경에서 로켓의 운동방정식 또는 추력 방정식은 다음과 같다.

 

 

$$ F = \dot{m} v_{e} + (p_{e} - p_{\infty}) S_{e}$$

로켓 추력 = 운동량 추력 + 입력 추력

여기서 $ \dot{m} $은 연소가스의 질량 유량(kg/s), $v_{e}$는 노즐 출구에서 연소가스의 배출 속도(m/s), $p_{e}$는 노즐 출구에서 연소가스의 압력(Pa), $p_{ \infty }$는 외기 압력(Pa), $S_{e}$는 노즐 출구의 면적(m²)이다.

 

[우주로켓] 로켓의 추진 성능