운동에는 거리와 변위보다 더 많은 물리량이 있다. "달리기 경주는 얼마나 걸리나요?", "주자의 속도는 얼마였나요?"와 같은 질문은 다른 개념의 이해 없이는 답할 수 없다. 여기에서는 시간, 속도, 속력에 대한 정의를 추가하여 운동에 대한 설명을 확장한다.
시간 (time)
앞서 <물리량과 단위>에서 설명한 것처럼 가장 기본적인 물리량은 측정 방법에 따라 정의된다. 시간도 마찬가지이다. 모든 시간 측정에는 어떤 물리량의 변화를 측정하는 것을 포함한다. 디지털시계의 숫자, 심장 박동, 하늘에서 태양의 위치 등이 그 대상이 될 수 있다. 물리학에서 시간(time)의 정의는 단순히 시간이란 변화, 즉 변화가 일어나는 간격이다. 무언가가 변하지 않으면 시간이 지났다는 것을 알 수 없다.
* 시간(時間): 어떤 시각에서 어떤 시각까지의 사이, 또는 시간의 어느 한 시점. =시각.
* 시각(時刻): 시간의 어느 한 시점
시간 또는 변화의 양은 기준과 비교하여 보정된다. 예를 들어 특정 진자가 0.75초마다 한 번씩 진동하는 것을 관찰할 수 있다. 그러면 진자의 진동 횟수를 세어 시간을 측정하거나 진자를 시간을 기록하는 시계 메커니즘에 연결하여 진자를 사용할 수 있다. 이를 통해 시간의 양을 측정할 수 있을 뿐만 아니라 일련의 이벤트도 파악할 수 있다.
시간은 운동과 어떤 관련이 있을까? 우리는 일반적으로 비행기 승객이 비행기 뒷좌석으로 이동하는 데 걸리는 시간과 같이 특정 동작의 경과 시간에 관심이 있다. 경과 시간을 찾으려면 운동의 시작과 끝의 시각을 기록하고, 이 둘을 빼면 된다. 예를 들어 강의가 오전 11:00에 시작하여 오전 11:50에 끝나면 경과 시간은 50분이다. 경과 시간 $ \Delta t$는 종료 시각과 시작 시각의 차이인 $ \Delta t = t_f - t_0$이며, 여기서 $ \Delta t $는 시간의 변화 또는 경과 시간, $ t_f $는 동작의 종료 시각, $ t_0 $는 동작의 시작 시각이다. (평소와 같이 델타 기호 $ \Delta $는 그 뒤에 오는 양의 변화를 의미한다.)
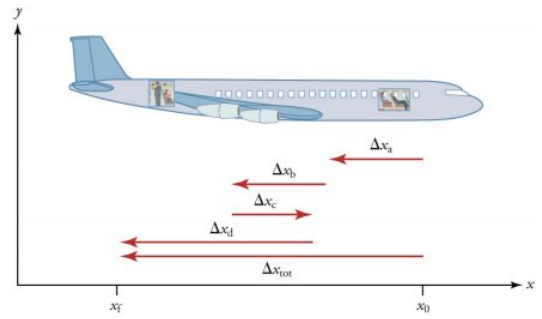
비행기 승객이 비행기 뒤쪽으로 향하는 모습을 더 자세히 기록하여 운동의 작은 부분을 나타낸다.
스톱워치를 사용할 때처럼 시작 시각 $t_0$을 0으로 잡으면 인생이 더 간단해진다. 스톱워치를 사용한다면 강의가 시작될 때 0, 끝날 때 50분이 표시될 것이다. $t_0 = 0$이면 $ \Delta t = t_f ≡ t$이다.
여기에서 간단하게 설명하기 위해, 운 동은 시간 0 에서 시작한다 ($ t_0 = 0$). 달리 명시되지 않는 한 경과 시간에는 기호 $ t$ 를 사용한다 ( $ \Delta t = t_f ≡ t$ ).
속도 (Velocity)
속도에 대한 여러분의 개념은 아마도 과학적 정의와 같을 것이다. 짧은 시간에 큰 변위가 있으면 속도가 크며, 속도는 시속 마일 또는 시속 킬로미터와 같이 거리를 시간으로 나눈 단위가 있다는 것을 알고 있을 것이다.
이 정의는 변위가 벡터이기 때문에 속도가 벡터임을 나타낸다. 속도에는 크기와 방향이 모두 있다. 속도의 SI 단위는 초당 미터 또는 m/s이지만 km/h, mi/h(mph라고도 표기), cm/s 등 다른 많은 단위를 일반적으로 사용한다. 예를 들어 비행기 승객이 -4m를 이동하는 데 5초가 걸렸다고 가정해 보자(음수 기호는 변위가 비행기 뒤쪽을 향하고 있음을 나타낸다). 그의 평균 속도는 다음과 같다.
$$ \bar{v} = {\Delta x \over t} = {-4m \over 5 s} = -0.8m $$
마이너스 기호는 평균 속도가 비행기의 뒤쪽을 향하고 있음을 나타낸다.
그러나 물체의 평균 속도는 시작 지점과 끝 지점 사이에서 물체에 어떤 일이 일어나는지에 대해서는 아무것도 알려주지 않는다. 예를 들어, 비행기 승객이 비행기 뒤편으로 가기 전에 잠시 멈췄는지 아니면 후진했는지는 평균 속도로는 알 수 없다. 더 자세한 정보를 얻으려면 더 작은 시간 간격으로 여행의 작은 구간을 고려해야 한다.
평균 속도는 변위 ( 위치 변화 ) 를 이동 시간으로 나눈 값이다 .
$$ \bar{v} = {\Delta x \over \Delta t} = {{x_f - x_0} \over {t_f - t_0}} $$
여기서 $ \bar{v}$는 평균 속도이고, $ \Delta x$는 위치의 변화(변위), $ x_f $와 $ x_0$는 각각 시간 $t_f$와 $t_0$에서의 마지막 위치와 시작하는 위치이다. 시작하는 시간 $t_0$이 0이라면, 평균 속도는 간단하게 다음과 같다.
$$ \bar{v} = {\Delta x \over t} $$
운동에서는 고려하는 시간 간격이 작을수록 더 자세한 정보를 얻을 수 있다 . 이 과정을 논리적 결론에 이르게 되면 무한히 작은 간격이 남게 된다 . 이러한 간격에서 평균 속도는 순간 속도 또는 특정 순간의 속도가 된다 . 예를 들어 자동차의 속도계는 자동차의 순간 속도의 크기 ( 방향은 표시하지 않는다 ) 를 보여준다 . ( 경찰은 순간 속도를 기준으로 티켓을 발부하지만 , 도로 여행에서 한 장소에서 다른 장소로 이동하는 데 걸리는 시간을 계산할 때는 평균 속도를 사용해야 한다 ). 순간 속도는 특정 순간 ( 또는 무한히 작은 시간 간격 ) 의 평균 속도이다 .
수학적으로 정확한 순간에 순간 속도 $v$ 를 구하려면 이 글의 범위를 벗어나는 미적분 연산인 극한을 구해야 할 수 있다 . 그러나 많은 상황에서 미적분 없이도 순간 속도의 정확한 값을 구할 수 있다.
속력 (Speed)
일상 언어에서 사람들은 대부분 속도(velocity)와 속력(speed)이라는 용어를 같은 의미로 사용한다. 그러나 물리학에서 속도와 속력은 같은 의미가 아니며, 엄연히 서로 다른 개념이다. 한 가지 큰 차이점은 속력에는 방향이 없다는 것이다. 따라서 속력은 스칼라이다. 순간 속도와 평균 속도를 구분해야 하는 것처럼, 순간 속력과 평균 속력도 구분해야 한다.
속도(速度): 물체의 단위 시간 내에서의 위치 변화. 크기와 방향이 있으며, 크기는 단위 시간에 지나간 거리와 같고, 방향은 경로의 접선과 일치한다.
속력(速力): 속도의 크기. 또는 속도를 이루는 힘
순간 속력은 순간 속도의 크기이다. 예를 들어, 어느 순간 비행기 승객의 순간 속도가 -3.0m/s(비행기 뒤쪽을 향한 마이너스를 의미)였다고 가정해 보자. 동시에 그의 순간 속력은 3.0m/s였다. 또는 쇼핑 여행 중 한 번에 순간 속도가 북쪽으로 40km/h라고 가정해 보자. 그 순간의 순간 속력은 40km/h로 같은 크기이지만 방향이 없다. 그러나 평균 속력은 평균 속도와 매우 다르다. 평균 속력은 이동한 거리를 경과 시간으로 나눈 값이다.
이동 거리가 변위 크기보다 클 수 있다는 점에 주목하자. 따라서 평균 속력은 변위를 시간으로 나눈 값인 평균 속도보다 클 수 있다. 예를 들어, 마트까지 운전해서 30분 만에 집으로 돌아왔는데 자동차의 주행 거리계에 전체 이동 거리가 6km로 표시되면 평균 속력은 12km/h이다. 그러나 왕복 거리의 변위가 0이기 때문에 평균 속도는 0이다. (변위는 위치의 변화이므로 왕복의 경우 0이다.) 따라서 평균 속력은 단순히 평균 속도의 크기가 아니다.
물체의 움직임을 시각화하는 또 다른 방법은 그래프를 사용하는 것이다. 위치 또는 속도를 시간의 함수로 나타낸 그래프는 매우 유용할 수 있다. 예를 들어, 이 상점까지의 이동에 대한 위치, 속도 및 속력 대 시간 그래프는 다음 그림에 표시하였다. (이 그래프는 이동의 매우 단순화된 모델을 나타낸다. 이동하는 동안 속력이 일정하다고 가정하는데, 이는 매장에 들르는 경우가 많다는 점을 고려할 때 비현실적인 가정이다. 하지만 단순화를 위해 정차나 속도 변화가 없는 것으로 모델링하였다. 또한 상점과 집 사이의 경로가 완벽한 직선이라고 가정한다.)
첫 번째 그래프는 시간에 따른 위치의 변화, 두 번째 그래프는 속도의 변화, 세 번째는 속력의 변화이다.
Access for free at openstax.org
OpenStax | Free Textbooks Online with No Catch
OpenStax offers free college textbooks for all types of students, making education accessible & affordable for everyone. Browse our list of available subjects!
openstax.org
'과학 > 물리학' 카테고리의 다른 글
| [물리학] 1차원에서 일정한 가속도를 위한 운동 방정식 (0) | 2024.06.02 |
|---|---|
| 가속도(Acceleration)란 무엇인가? (1) | 2024.06.02 |
| [물리학] 벡터, 스칼라, 그리고 좌표계 (0) | 2024.06.01 |
| [물리학] 변위와 거리 (0) | 2024.06.01 |
| [물리학] 측정 도구의 정밀도 및 유효 숫자 (0) | 2024.05.27 |