고정 헤더 영역
상세 컨텐츠
본문
다음 그림에 표시된 일반적인 고무 재료의 응력 - 변형률 거동은 탄성이지만 강한 비선형성을 가진다 .
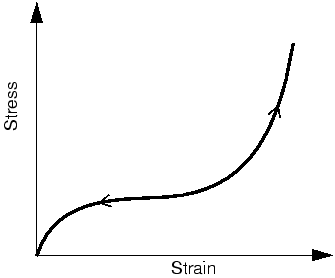
이 종류의 재료 모델은 초탄성(超彈性)이라고 한다. 고무 등의 초탄성 재료의 변형은 대변형 값까지 탄성을 유지한다. 가끔 100% 이상이다.
Abaqus는 초탄성 재료를 모델링할 때 다음 가정을 따른다.
• 재료 모델은 탄성이다.
• 재료 모델은 등방성이다.
• 해석은 비선형 기하학적 효과를 고려한다.
또한 Abaqus/Standard는 기본적으로 초탄성 재료가 압축되지 않은 것으로 가정한다. Abaqus/Explicit는 재료가 거의 압축되지 않는다고 가정한다. 기본 푸아송의 비는 0.475이다.
탄성 발포 재료는 다른 비선형성이 강한 탄성 재료이다. 이들은 압축 하중을 받았을 때 매우 높은 압축 거동을 나타내는 점이 고무 재료와 다르다. 이들은 Abaqus에서 다른 재료 모델로 만들며, 이 책에서는 세부 사항을 다루지 않는다.
1) 압축성
대부분의 고체 고무 재료는 전단 변형보다 압축성이 거의 없다. 이 거동은 평면 응력 요소, Shell 요소, Membrane 요소에서 문제가 되지 않는다. 하지만 평면 변형률 요소, 축대칭 요소, 3차원 Solid 요소 등을 사용하면 문제가 될 수 있다. 예를 들어, 재료의 구속이 약한 문제에서 재료가 완벽히 비압축성이라고 가정하는 것은 매우 합리적이다. 이 경우 열팽창을 제외하고, 재료의 부피는 변할 수 없다. 재료가 강하게 구속되는 문제(틈새를 막는 데 사용하는 오링 등)는 정확한 결과를 얻으려면 압축성을 정확하게 만들어야 한다.
Abaqus/Standard는 초탄성 재료에서 볼 수 있는 완전 비압축성 거동을 해석할 때 사용하는 특별한 ‘하이브리드’ 요소를 제공한다. 이런 ‘하이브리드’ 요소는, 이름의 문자 'H'로 식별된다. 예를 들어, 8절점 6면체 요소(C3D8)의 하이브리드 형식은 C3D8H라고 한다.
Abaqus/Explicit에서 재료가 완벽히 압축되지 않은 구속조건을 적용하는 메커니즘이 없으므로 평면 응력과 단축을 제외하고 압축되지 않은 조건을 가정할 수 없다. 또한, 비압축성 재료는 무한한 소밀파 속도를 가지며, 결과적으로 시간 증분이 ‘0’이 된다. 따라서, 어느 정도의 압축성을 적용할 필요가 있다. 가끔 문제는 실제 재료에서 압축성이 매우 작아서 알고리즘이 효율적으로 작동하지 않는다는 것이다. 따라서, 평면 응력과 단축의 경우를 제외하고, 모델의 체적 거동이 실제 재료의 체적 거동보다 부드러워진다는 것을 알고 나서, 프로그램이 기능하기에 충분한 압축성을 적용할 필요가 있다. 따라서 이 수치 해석에 대한 제한으로 충분한 정밀 해를 얻을 수 있는지, Abaqus/Explicit에서 문제를 만들 수 있는지를 결정해야 한다. 재료의 상대 압축성은 재료의 초기 전단 탄성률에 대한 초기 체적 탄성률($ K_0 $)의 비율로 평가할 수 있다. 또한 푸아송의 비($ \nu $)는 다음과 같이 정의하므로 압축성을 측정한다.
$$ \nu = {{3 \left ( K_{0} / \mu_{0} \right) - 2} \over {6 \left ( K_{0} / \mu _{0} \right) + 2}} $$
다음 표는 몇 가지 대표적인 값이다.
표. 압축성과 푸아송의 비 사이의 관계
| $ K_0 / \nu_0 $ | 푸아송의 비 |
| 10 | 0.452 |
| 20 | 0.475 |
| 50 | 0.490 |
| 100 | 0.495 |
| 1,000 | 0.4995 |
| 10,000 | 0.49995 |
재료 압축성에 값을 지정하지 않으면, 기본적으로 Abaqus/Explicit가 푸아송의 비가 0.475이므로 $ K_0 / \nu_0 $ =20으로 가정된다. 일반적인 미충전 탄성 고무의 $ K_0 / \nu_0 $ 비율은 1,000~10,000 범위($\nu$=0.4995에서 $\nu$ =0.49995)이며, 충전 탄성 고무의 $ K_0 / \nu_0 $ 비율은 50~200의 범위($\nu$ =0.490에서 $\nu$ =0.497)이므로, 이 기본값은 대부분 탄성 고무에서 얻은 압축성보다 훨씬 더 높은 압축성을 제공한다. 하지만 탄성 고무가 너무 많이 제한되지 않으면 재료의 체적 거동을 매끄럽게 만들더라도 일반적으로 상당히 높은 정확성의 결과를 얻을 수 있다. 그러나 그 재료가 상당히 정확하게 구속되어 있으면(재료가 단단한 금속 부품과 접촉하고, 자유로운 표면이 매우 작은 경우나, 특히 높은 압축 하중을 받는 경우 등), Abaqus/Explicit로 정밀한 결과 얻는 것은 불가능하다.
Abaqus/Explicit에서 기본값을 그대로 사용하지 않고 압축성을 정의할 때 $ K_0 / \nu_0 $ 비율에 대해 100의 상한값을 권장한다. 이보다 큰 비율을 사용하면 동적 해에 고주파 노이즈가 들어가므로 지나치게 작은 시간 증분을 사용해야 한다.
2) 변형률 에너지 포텐셜
Abaqus는 영률과 푸아송의 비가 아닌 변형률 에너지 포텐셜($U$)을 사용하여 초탄성 재료의 응력을 변형률에 연결한다. 여러 가지 변형률 에너지 포텐셜(다항식 모델, Ogden 모델, Arruda-Boyce 모델, Marlow 모델, Van der Waals 모델)을 사용할 수 있다. Mooney-Rivlin 모델, neo-Hookean 모델, 감소 다항식 모델과 Yeoh 모델도 다항식 모델의 더 간단한 형식으로 사용할 수 있다.
다항식 형식의 변형률 에너지 포텐셜은 자주 사용하는 변형률 에너지 포텐셜이다. 이 형식은 다음과 같다.
$$ U = \sum_{i+j=1}^{N} C_ij \left (\bar {I}_1-3 \right)^i \left ( \bar {I}_2-3 \right)^j + \sum_{i=1}^{N} {{1} \over {D_i}} \left (J_{el}- 1 \right)^{2i} $$
여기서 $U$는 변형률 에너지 포텐셜, $ J_{el} $은 탄성 체적비, $ \bar {I}_1 $과 $ \bar {I}_2 $ 는 재료 변형의 측정, $N$, $ C_{ij} $, $ D_i $는 재료 파라미터(온도의 함수일 수 있다.)이다. $ C_{ij} $변수는 재료의 전단 거동, $ D_i $변수는 압축성을 나타낸다. 재료가 완전 비압축성이면(Abaqus/Explicit에서 사용할 수 없는 조건), $ D_i $의 값은 모두 ‘0’으로 설정하며, 위 식의 두 번째 항은 무시한다. 항의 수 $N$ 이 1이면, 초기 전단 탄성률($ \mu_0 $)과 초기 체적 탄성률($ K_0 $)은 다음과 같다.
$$ \mu_{0} = 2 \left (C_{01}+C_{10} \right), K_0 = {2 \over D_1} $$
또한 재료가 비압축성일 때 변형 에너지 밀도의 공식은 다음과 같다.
$$ U=C_{10} \left ({\bar{I_{1}}}-3 \right)+C_{01} \left({\bar{I_{2}}}-3 \right) $$
이 공식은 일반적으로 Mooney-Rivlin 재료 모델이라고 한다. 게다가 $ C_{01} $이 ‘0’이면 재료는 neo-Hookean 모델이라고 한다.
초탄성 재료를 사용하려면 Abaqus에 관련 재료 변수를 입력해야 한다. 다항식 형식에서 관련 재료 변수는 $ C_{ij} $와 $ D_i $이다. 초탄성 재료를 입력할 때 이 변수를 제공할 수 있다. 하지만 해석해야 하는 재료에 가끔 시험 데이터가 제공된다. Abaqus는 시험 데이터를 그대로 입력하고, 재료 변수를 계산할 수 있다. 최소 제곱 근사를 사용한다.
3) 시험 데이터에 의한 초탄성 거동의 정의
초탄성 재료를 정의하는 편리한 방법은 Abaqus에 시험 데이터를 입력하는 것이다. 이 경우 Abaqus는 최소 제곱법을 사용하여 상수를 계산한다.
Abaqus는 다음 시험 데이터를 근사할 수 있다.
• 단축 인장과 압축
• 2축 균등 인장과 압축
• 평면 인장과 압축(순 전단)
• 부피에 대한 인장과 압축
이런 시험에서 볼 수 있는 변형 모드는 다음 그림과 같다. 소성 데이터와 달리 초탄성 재료의 시험 데이터는 공칭 응력과 공칭 변형률로 Abaqus에 제공한다.
체적 압축 데이터는 재료의 압축성이 중요한 경우만 제공되어야 한다. 일반적으로 Abaqus/Standard는 재료의 압축성은 중요하지 않으며, 디폴트 완전 비압축 거동이 사용된다. 앞서 언급했듯이 Abaqus/Explicit는 체적 시험 데이터를 주지 않으면 약간의 압축성으로 가정한다.
초탄성 재료를 사용한 해석 결과의 품질은 Abaqus가 제공하는 재료 시험 데이터에 크게 의존한다. 대표적인 시험은 다음 그림에 나와 있다. Abaqus가 가능한 최상의 재료 변수를 계산할 수 있도록 사용자가 할 수 있는 몇 가지 사항이 있다.
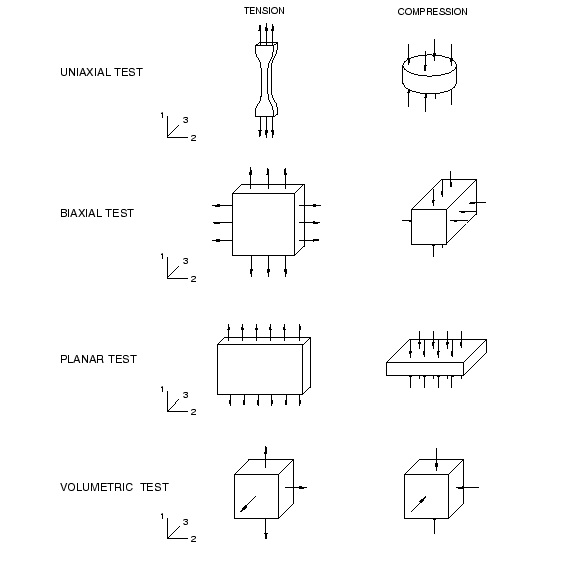
가능한 한 시험 데이터는 두 가지 이상의 변형 상태에서 얻어야 한다. 이렇게 하면 Abaqus는 더 정확하고 안정적인 재료 데이터를 만들 수 있다. 하지만 그림에 표시된 일부 시험은 비압축성 재료에 동등한 변형 모드를 제공한다.
다음은 비압축성 재료와 동등한 시험이다.
• 단축 인장 ↔ 2축 균등 압축
• 단축 압축 ↔ 2축 균등 인장
• 평면 인장 ↔ 평면 압축
이미 특정 변형 모드를 만드는 시험 데이터가 있다면 다른 시험 데이터를 포함할 필요가 없다.
또한, 다음은 초탄성 재료 모델을 개선할 수 있다.
- 해석에서 발생할 가능성이 큰 변형 모드에서 시험 데이터를 얻는다. 예를 들어 구성 요소가 압축 하중을 받으면 시험 데이터에 인장이 아닌 압축 하중이 포함된다.
- 압축 응력과 변형률을 음수 값으로 입력하면, 인장과 압축 데이터를 모두 사용할 수 있다. 인장과 압축 데이터 모두에 단일 재료 모델을 근사하면 시험에 근사보다 정확도가 떨어지므로 가능한 경우 문제에 따라 압축 또는 인장 전용 데이터를 사용한다.
- 평면 시험의 시험 데이터를 포함한다. 이 시험은 전단 거동을 측정한다. 이 거동은 매우 중요할 수 있다.
- 해석 중에 재료에 발생할 것으로 예상되는 변형률의 크기로 더 많은 데이터를 제공한다. 예를 들어, 재료의 인장 변형률이 50% 미만이면 대변형 값(100% 이상)으로 시험한 데이터가 있더라도 가능한 한 제공하지 않는다.
- Abaqus/CAE의 재료 평가 기능을 사용하여 실험 시험의 해석을 시행하고 Abaqus가 계산한 결과를 시험 데이터와 비교한다. 중요한 특정 변형 모드의 계산 결과가 좋지 않으면 해당 변형 모드에 대한 시험 데이터를 더 많이 얻으려고 노력한다.
시험 데이터에서 얻은 초탄성 재료 모델은 특정 변형률의 크기로 불안정해질 수 있다. Abaqus는 안정성 검사를 수행하여 불안정한 동작이 발생하는 왜곡의 크기를 결정하고 데이터 파일(.dat)에 경고 메시지를 출력한다. 같은 정보가 Abaqus/CAE에서 재료 평가 기능을 사용할 때 나타나는 Material Parameters and Stability Limit Information 대화 상자에 나타난다. 모델에서 변형이 이 안정 한계를 초과하면 해석이 현실적이지 않을 수 있으므로 이 정보를 주의 깊게 확인해야 한다. 이 안정성 검사는 특정 변형에서 수행한다. 따라서 변형이 더욱 복잡해지면 표시된 변형 수준을 낮추더라도 재료가 불안정해질 수 있다. Abaqus/Standard에서 모델에 안정성 한계를 초과하는 부분이 있으면 해석이 수렴하지 않을 수 있다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 큰 왜곡에 대한 요소망 분할 (0) | 2024.06.01 |
|---|---|
| [Abaqus] 예제: 축대칭 마운트 (0) | 2024.06.01 |
| [Abaqus] 예제: 보강된 판에 대한 폭풍 하중 (0) | 2024.05.31 |
| [Abaqus] 예제: 소성을 고려한 연결용 러그 (0) | 2024.05.31 |
| [Abaqus] 탄소성 문제의 요소 선택 (0) | 2024.05.31 |




