고정 헤더 영역
상세 컨텐츠
본문
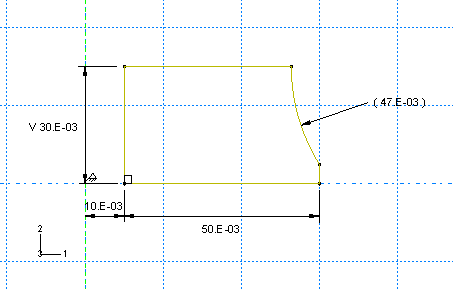
다음 그림에 표시된 고무 마운트의 축 방향 강성을 구하고 마운트의 피로 수명에 영향을 미치는 최대 주응력이 큰 영역을 식별한다. 이 마운트는 양단이 강판에 접합되어 있다. 이 마운트는 강판 전체에 걸쳐 균일하게 분포되는 최대 5.5 kN의 축 방향 하중이 작용한다. 단면의 형상과 치수는 다음 그림과 같다.
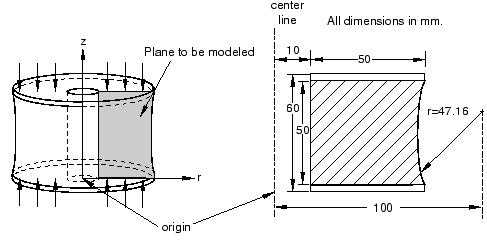
구조의 모양과 하중은 모두 축대칭이므로 이 해석에서 축대칭 요소를 사용할 수 있다. 따라서 이 구성 요소의 축대칭 평면만 만들어야 한다. 각 요소는 완전한 360° 링을 나타낸다. 마운트의 정적 응답을 조사하므로 이 해석은 Abaqus/Standard를 사용한다.
1) 대칭성
이 문제는 마운트의 중심을 통과하는 수평선에 대칭이므로 전체 축대칭 평면을 만들 필요는 없다. 이 축대칭 평면의 절반만을 만들면 사용하는 요소의 수가 절반이 되면 자유도 수가 거의 절반이 된다. 이렇게 하면 해석 실행 시간과 저장 공간 요구 사항이 크게 줄어든다. 또한 요소망을 더 미세하게 만들 수 있다.
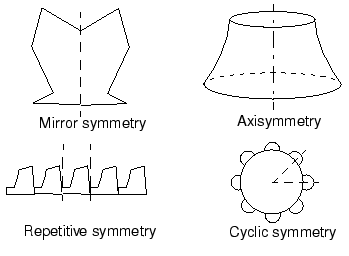
많은 문제에서 어느 정도의 대칭이 포함된다. 예를 들어, 다음 그림과 같이 대칭, 주기 대칭, 축대칭, 반복 대칭이 일반적이다. 해석할 구조과 구성 요소에는 다양한 대칭이 있을 수 있다.
대칭 구성 요소를 일부분만 만들 때 모델의 동작이 전체 구성 요소를 만든 것과 같도록 경계 조건을 추가해야 한다. 또한 적용하는 하중은 실제로 만든 일부 구조물을 반영하도록 조정해야 한다. 다음 그림의 게이트 프레임을 생각해 보자.
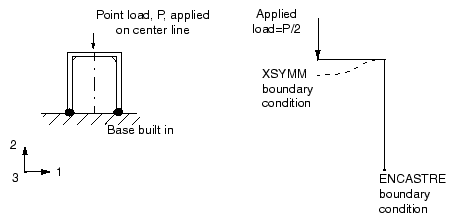
이 프레임은 그림에 표시된 수직선에 대칭이다. 이 모델의 대칭성을 유지하려면 대칭 선의 모든 절점을 1방향 이동과 2축과 3축 중심의 회전이 일어나지 않도록 구속해야 한다.
이 프레임 문제에서 하중은 모델의 대칭 평면을 따라 적용한다. 따라서 해석할 부분은 전체 값의 절반만 제공한다.
이 고무 마운트 예제와 같이 축대칭 요소를 사용한 축대칭 해석은 구성 요소의 단면만 만들어야 한다. 이 요소의 공식화는 축대칭 효과를 자동으로 고려한다.
2) 전처리
축대칭 변형 Shell 파트를 만든다. 파트에 Mount라는 이름을 입력하고 파트의 근사 크기에 0.3을 입력한다. 대칭성을 고려하여 마운트의 하반부만 만든다. 다음 권장 방법을 사용하여 파트의 기하 형상을 만들 수 있다. 먼저 Sketcher를 시작하면 고정된 배치 제한을 나타내는 녹색 점선으로 회전축이 표시된다. 스케치는 이 축을 가로지를 수 없다.
마운트 기하 형상을 스케치하려면 다음과 같이 설정한다.
1. 대칭축의 오른쪽에 어떤 크기의 직사각형을 그린다. 이것은 다음과 같이 치수를 입력한다. 대칭축과 직사각형의 왼쪽 가장자리 사이의 수평 거리를 0.01 m로 입력한다. 직사각형의 수직 높이를 0.030 m, 수평 스팬을 0.050 m로 입력한다.
2. Create Circle: Center and Perimeter 도구를 사용하여 원을 스케치한다. 원의 중심으로 직사각형의 오른쪽에 있는 어떤 위치를 선택하고 둘레를 직사각형의 오른쪽 가장자리의 어떤 위치로 지정한다. 이 원에 다음과 같이 치수를 입력한다. 대칭축과 원 중심 사이의 수평 거리를 0.1 m로 입력한다. 원의 중심과 직사각형의 오른쪽 위 꼭짓점 사이의 수직 거리를 0 m로 입력한다. 외주 점(원이 직사각형과 교차하는 곳)과 직사각형의 오른쪽 아래 꼭짓점 사이의 수직 거리를 0.005 m로 설정한다. 이 스케치는 다음 그림에 나와 있다.
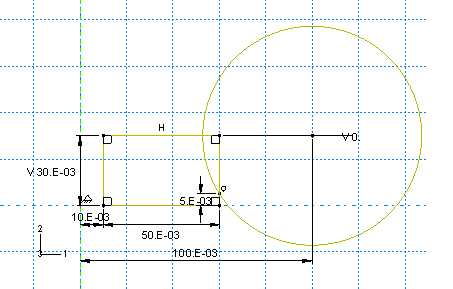
3. Auto-Trim 도구를 사용하여 다음 그림과 같이 스케치의 나머지 부분을 제거한다.
이 마운트에 사용하는 고무 재료는 몇 가지 재료 시험 데이터를 제공한다. 단일 축 시험, 2축 균등 시험, 평면(전단) 시험의 세 가지 시험 데이터가 있다. 이 데이터는 공칭 응력과 그에 상응하는 공칭 변형률로 제공된다.
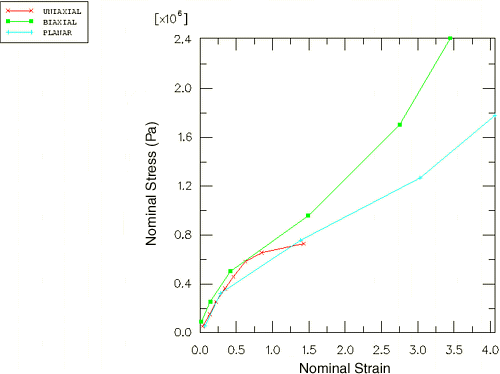
표. 단축 시험 데이터
| 응력(Pa) | 변형률 |
| 0.054E6 | 0.0380 |
| 0.152E6 | 0.1338 |
| 0.254E6 | 0.2210 |
| 0.362E6 | 0.3450 |
| 0.459E6 | 0.4600 |
| 0.583E6 | 0.6242 |
| 0.656E6 | 0.8510 |
| 0.730E6 | 1.4268 |
표. 2축 균등 시험 데이터
| 응력(Pa) | 변형률 |
| 0.089E6 | 0.0200 |
| 0.255E6 | 0.1400 |
| 0.503E6 | 0.4200 |
| 0.958E6 | 1.4900 |
| 1.703E6 | 2.7500 |
| 2.413E6 | 3.4500 |
표 . 평면 시험 데이터
| 응력(Pa) | 변형률 |
| 0.055E6 | 0.0690 |
| 0.324E6 | 0.2828 |
| 0.758E6 | 1.3862 |
| 1.269E6 | 3.0345 |
| 1.779E6 | 4.0621 |
⊙ 체적 시험 데이터는 재료가 비압축성일 때 필요하지 않다.
시험 데이터를 사용하여 초탄성 재료를 정의하려면, 데이터에 적용하는 변형률 에너지 포텐셜도 지정한다. Abaqus는 시험 데이터를 사용하여, 지정된 변형률 에너지 포텐셜에 필요한 계수를 계산한다. 재료 특성 정의에서 예측된 행동과 시험 데이터가 허용할 수 있는 범위에서 일치하는지 확인하는 것이 중요하다.
Abaqus/CAE에서 사용할 수 있는 재료 평가 옵션을 사용하여 시험 데이터를 사용하여 하나 이상의 표준 시험을 재료 정의에 지정된 변형률 에너지 포텐셜을 사용하여 해석할 수 있다.
초탄성 재료 모델을 정의하고 평가하려면 다음과 같이 설정한다.
1. 초탄성 재료 Rubber를 만든다. 이 예제에서 1차 다항식 변형률 에너지 함수를 사용하여 고무 재료를 만든다. 즉, 재료 특성 편집 대화 상자의 Strain energy potential 목록에서 Polynomial을 선택한다. 재료 특성 편집 대화 상자의 Test Data 메뉴 항목을 사용하여 이전에 표시된 시험 데이터를 입력한다. 시험 데이터를 표시하려면, 시험 데이터를 마우스 버튼 3으로 클릭하고, 표시되는 메뉴에서 Create X–Y Data를 선택한다. 이에 따라 Visualization 모듈에서 데이터를 표시할 수 있다.
◉ 일반적으로 지정된 변형률 에너지 포텐셜이 결정되지 않을 수 있다. 이 경우 재료 특성 편집 대화 상자의 Strain energy potential 목록에서 Unknown을 선택할 수 있다. 그다음 Evaluate 옵션을 사용하여 시험 데이터를 사용하여 표준 시험을 여러 변형률 에너지 포텐셜을 사용하여 선택하고 선택 지침으로 사용할 수 있다.
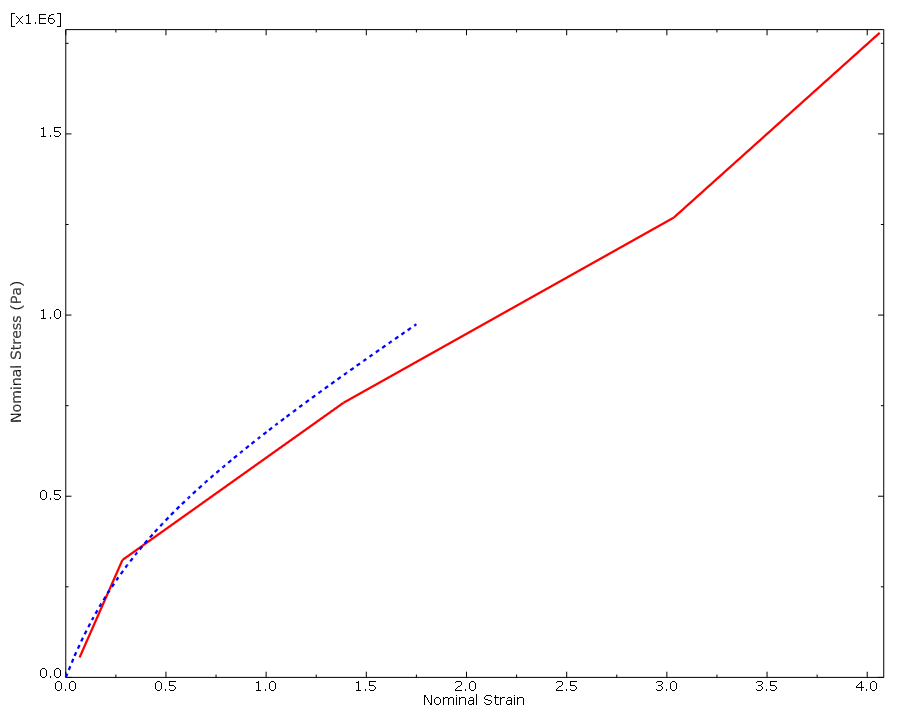
2. 모델 트리에서 Materials 컨테이너 아래에 있는 Rubber를 마우스 버튼 3으로 클릭한다. 표시된 메뉴에서 Evaluate를 선택하고, 표준 단위요소 시험(단축, 2축 균등, 평면)을 시행한다. 각 시험의 최소 변형에 0, 최대 변형에 1.75를 입력한다. 다음 1차 다항식 변형 에너지 함수만 평가한다. 이 형태의 초탄성 모델은 Mooney-Rivlin 재료 모델로 알려져 있다. 평가가 완료되면 Abaqus/CAE는 Visualization 모듈을 시작한다. 재료 변수와 안정성 정보를 포함하는 대화 상자가 나타난다. 또한 재료의 공칭 응력-공칭 변형률 곡선을 나타내는 X-Y 표시와 시험 데이터 표시가 각 시험에 표시된다.
각 종류의 시험을 계산한 결과와 실험 결과를 다음 그림에서 비교한다(편의를 위해 일부 계산 데이터 포인트는 표시되지 않음). 2축 인장 시험에서 Abaqus/Standard의 결과와 실험 결과는 매우 잘 일치한다. 단축 인장 시험과 평면 시험에서 계산 결과와 실험 결과가 변형률이 100% 미만일 때 잘 일치한다. 이런 재료 시험 데이터에서 생성된 초탄성 재료 모델은 변형률이 100% 이상인 해석에서 사용하기에 적합하지 않은 것으로 간주한다. 그러나 이 해석에서 시험 데이터와 초탄성 모델이 잘 일치하는 변형 범위 내에 주변형이 유지되면 이 재료 모델로 충분하다. 해석 결과가 이 값을 초과하거나 다른 해석을 수행해야 하는 경우 더 나은 재료 데이터를 요청해야 한다. 그렇지 않으면 얻은 결과를 신뢰할 수 없다.
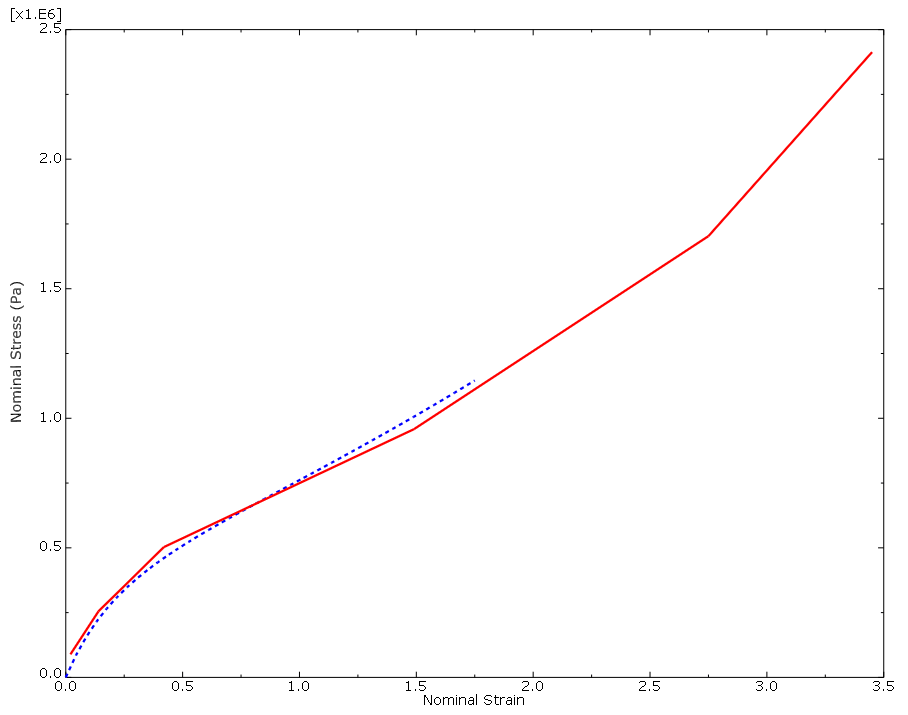
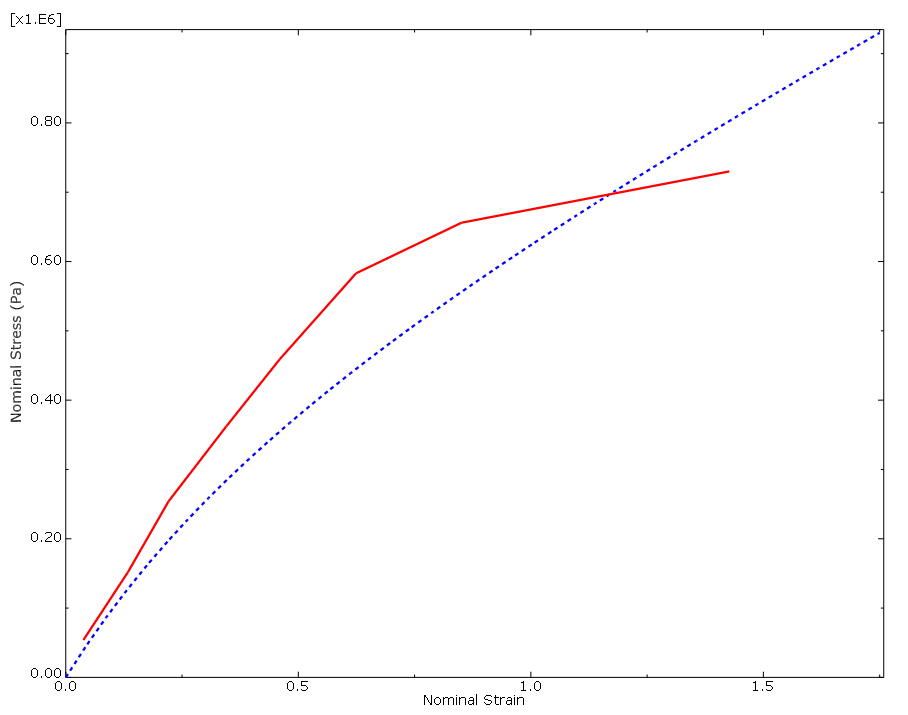
이 해석에서 재료는 비압축성이라고 가정($D_1 =0$)한다. 체적 시험 데이터는 제공하지 않는다. 압축성 거동을 해석할 때 체적 시험 데이터를 다른 시험 데이터에 추가해야 한다.
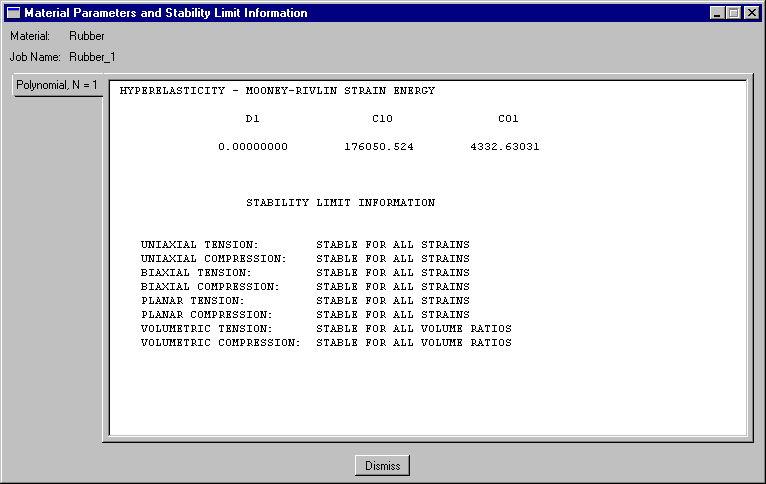
다음 그림과 같이 Abaqus가 재료 시험 데이터에서 계산하는 초탄성 재료 계수($ C_{10} $, $ C_{01} $, $ D_{1} $)는 Material Parameters and Stability Limit Information 대화 상자에 표시된다. 이 재료 모델은 이 재료 시험 데이터와 이 변형률 에너지 함수에 대해 모든 변형에서 안정적이다.
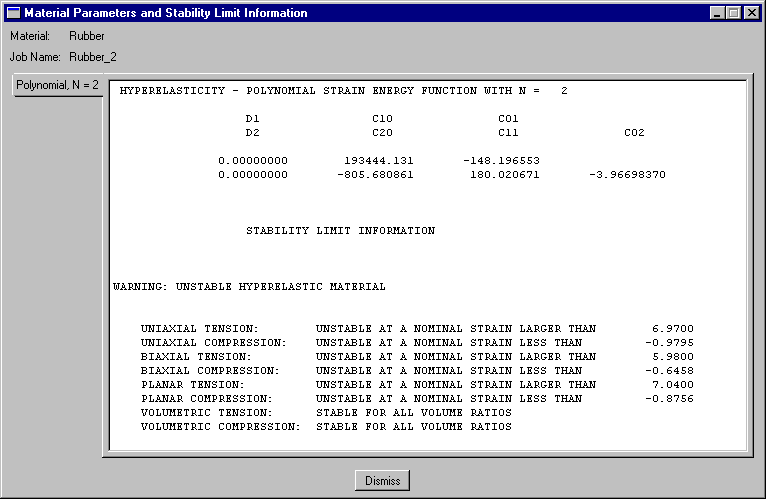
그러나 2차(N=2) 다항식 변형률 에너지 함수의 사용을 지정하면 다음 그림에 표시된 경고가 표시된다. 이 문제에서 단축 시험 데이터만 제공하면 Abaqus에서 만든 Mooney-Rivlin 재료 모델은 일정한 변형 값을 초과하면 불안정한 재료 모델이 된다.
하중은 비탄성 변형을 일으키는 만큼 크지 않기 때문에, 강철 재료는 선형 탄성으로 만든다($E$=200×109Pa, $ \nu $=0.3). 이 특성을 가진 재료 Steel을 만든다. 고무 재료를 참조하는 요소 특성 정의 Rubber_Section과 강철 재료를 참조하는 요소 특성 정의 Steel_Section을 작성한다.
요소 특성을 지정하기 전에 Partition Face: Sketch 도구를 사용하여 파트를 다음 그림에 표시된 두 영역으로 나눈다.

Sketcher에서 원호가 오른쪽 가장자리와 교차하는 위치에서 스케치의 왼쪽 가장자리를 넘는 임의의 위치까지 수평선을 그린다.
상부 영역은 고무 마운트를 표현하고, 하부 영역은 강판을 표현한다. 대응하는 요소 특성 정의를 각 영역에 지정한다.
파트의 dependent Instance를 만든다. 이 해석에서는 기본 $ r-z $(1-2) 축대칭 좌표계를 그대로 사용할 수 있다. 그다음 정적 일반 단계 Compress mount를 정의한다. 초탄성 재료가 모델에서 사용되면 Abaqus는 모델이 대변형을 겪는다고 가정한다. 그러나 Abaqus/Standard에서 대변형과 같은 기하 비선형 효과는 기본적으로 고려되지 않는다. 따라서 Nlgeom을 켜면 이 해석에 기하 비선형 효과를 포함할 수 있다. 그렇지 않으면 Abaqus/Standard는 입력 오류를 출력하여 해석을 중단한다. 시간 폭을 1.0으로 설정하고 초기 시간 증분을 0.01(전체 단계 시간의 1%)로 설정한다.
출력을 제한하려면 강판 영역의 왼쪽 아래 모서리에 있는 꼭짓점에 형상 세트 Out을 만든다.
사전 선택 변수와 공칭 변형률을 필드 출력으로 ODB 파일에 증분별로 내보낸다. 또한 마운트의 강성을 계산할 수 있도록 강판 밑면의 한 점에서 변위를 ODB 파일에 데이터로 기록한다. 이를 위해 기하 형상 세트 Out을 사용한다.
대칭 평면의 영역에 경계 조건을 지정한다(U2=0은 다음 그림에 나와 있다. 이 예는 YSYMM과 같다).
모델의 축대칭 특성으로 구조물은 반경 방향(글로벌 1축)으로 강제 이동할 수 없으므로 반경 방향(전체 첫 번째 방향)의 경계 제한이 필요하지 않다. 절점은 반경 방향 변위(자유도 1)에 경계 조건이 적용되지 않으면 초기 형상이 대칭축에 있는 경우(반경 방향 좌표가 0.0인 경우)를 포함하여 반경 방향으로 이동할 수 있다. 이 해석에서 마운트는 반경 방향으로 변형되므로 경계 조건을 지정하면 안 된다. 다시 말하지만, 강체 운동은 Abaqus가 자동으로 구속한다.
마운트는 강판의 전면에 균일하게 분포하는 5.5 kN의 최대 축 하중을 유지한다. 따라서 위 그림과 같이 분포 하중은 강판의 밑면에 입력한다. 이 압력의 크기는 다음과 같다.
$$ p=5500/ \left (\pi \left (0.06^{2}-0.01^{2} \right) \right) \cong 0.50 \times 10^{6} \rm Pa $$
1차 축대칭 하이브리드 Solid 요소(CAX4H)를 고무 마운트에 사용한다. 이 재료는 완전 비압축성이므로 하이브리드 요소를 사용해야 한다. 이 요소는 휘어지지 않으리라고 예상되므로 이런 완전 적분 요소의 전단 잠금은 문제가 되지 않는다. 강판은 그 아래의 고무 변형에 따라 휘어질 수 있으므로 단일 레이어의 부적합 모드 요소(CAX4I)로 만든다.
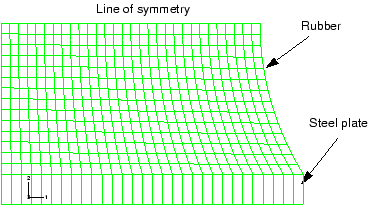
4각형 요소망을 만든다. 가장자리 방향의 요소 수를 지정하여 파트에 Seed를 정의한다(Seed → Edges). 각 수평 에지에 30요소, 고무의 수직 에지와 곡선 에지에 14요소, 강판의 수직 에지에 1요소를 지정한다. 이 요소망은 다음 그림과 같다.
작업 Mount를 만든다. 작업 설명에 Axisymmetric mount analysis under axial loading을 입력한다.
모델을 모델 데이터베이스 파일에 저장하고 해석 작업을 제출한다. 해석 진행 상황을 관찰하고, 모델링 오류가 감지되면 이를 수정하고, 경고 메시지가 있는 경우 원인을 조사한 다음 필요에 따라 수정한다.
3) 후처리
Visualization 모듈을 시작하고 Mount.odb 파일을 연다. 주어진 하중의 함수로서 강판의 변위를 X-Y 표시하여 마운트의 강성을 구한다. 먼저 ODB 파일에 데이터를 내보낸 강판 절점의 수직 변위를 표시한다. 데이터는 이 모델의 세트 Out 절점에 기록된다.
수직 변위의 이력 곡선을 만들고 X축과 Y축을 바꾸려면 다음과 같이 설정한다.
1. 결과 트리에서 출력 데이터베이스 Mount.odb 아래의 History Output 컨테이너를 확장한다.
2. 세트 Out 절점에서 수직 방향 변위 U2를 찾아 선택한다.
3. 마우스 버튼 3을 클릭하고 표시된 메뉴에서 Save As를 선택하여 X-Y 데이터를 저장한다. Save XY Data As 대화 상자가 나타난다.
4. Save XY Data As 대화 상자가 나타나면 곡선에 SWAPPED라고 이름을 입력하고 저장 조작으로 swap(XY)을 선택하고 OK를 클릭한다. 시간-변위 표시가 뷰포트에 표시된다.
이제 시간 변위 곡선이 얻어졌다. 필요한 것은 힘 변위를 나타내는 곡선이다. 이 해석에서 마운트에 주어진 힘은 해석의 전체 시간에 정비례하므로 이 곡선을 만드는 것은 간단하다. 힘-변위 곡선을 표시하는 데 필요한 작업은 곡선 SWAPPED에 하중 크기(5.5 kN)를 곱하는 것이다.
곡선에 일정 값을 곱하려면 다음과 같이 설정한다.
1. 결과 트리에서 XYData를 두 번 클릭한다. Create XY Data 대화 상자가 나타난다.
2. Operate on XY data을 선택하고 Continue를 클릭한다. Operate on XY Data 대화 상자가 나타난다.
3. XY Data 필드에서 SWAPPED를 두 번 클릭한다. 산술식 ‘SWAPPED’는 대화 상자의 상단에 있는 텍스트 필드에 표시된다. 커서는 텍스트 필드의 끝에 있다.
4. *5500을 입력하여 텍스트 필드의 데이터 객체에 하중 값을 곱한다.
5. 대화 상자 아래쪽의 Save As를 클릭하여 곱한 데이터 개체를 저장한다. Save XY Data As 대화 상자가 나타난다.
6. Name 텍스트 필드에 FORCEDEF를 입력하고 OK를 클릭하여 대화 상자를 닫는다.
7. 힘-변위 표시를 보려면 Operate on XY Data 대화 상자의 아래쪽에 있는 산술식 표시를 클릭한다.
이제 마운트의 힘-변위 특성 곡선이 만들어졌다(축 레이블은 변경되지 않았기 때문에 표시된 실제 변수를 반영하지 않는다). 강성을 얻으려면 곡선 FORCEDEF를 미분해야 한다. 이것은 Operate on XY Data 대화 상자의 differentiate() 연산자를 사용하여 수행할 수 있다.
강성을 얻으려면 다음과 같이 설정한다.
1. Operate on XY Data 대화 상자에서 현재 산술식을 지운다.
2. Operators 목록에서 differentiate(X)를 클릭한다. differentiate()는 대화 상자의 맨 위에 있는 텍스트 필드에 표시된다.
3. XY Data 필드에서 FORCEDEF를 두 번 클릭한다. 산술식 differentiate( "FORCEDEF")가 텍스트 필드에 표시된다.
4. 대화 상자 아래쪽에 있는 Save As를 클릭하여 미분된 데이터 개체를 저장한다. Save XY Data As 대화 상자가 나타난다.
5. Name 텍스트 필드에 STIFF를 입력하고 OK를 클릭하여 대화 상자를 닫는다.
6. 강성-변위 곡선을 표시하려면, Operate on XY Data 대화 상자의 아래쪽에 있는 산술식 표시를 클릭한다.
7. Cancel을 클릭하여 대화 상자를 닫는다.
8. Axis Options 대화 상자를 열고 Title 탭으로 전환한다.
9. 다음 그림과 같이 축 제목을 사용자 정의한다.
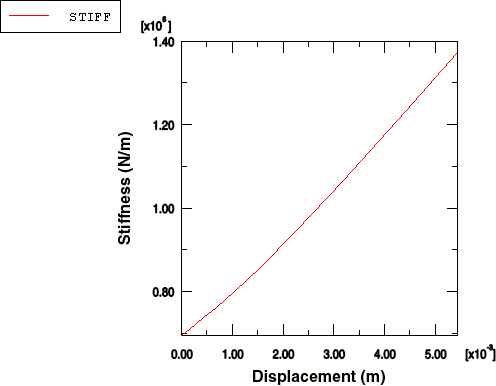
10. Dismiss를 클릭하여 Axis Options 대화 상자를 닫는다.
마운트의 강성은 마운트가 변형되면 거의 100% 증가한다. 이것은 마운트가 변형될 때 고무의 비선형성과 마운트 모양 변화의 결과이다. 또 다른 방법은 위의 모든 연산자를 하나의 산술식으로 결합하여 강성-변위 곡선을 직접 만들 수도 있다.
강성 곡선을 직접 정의하려면 다음과 같이 설정한다.
1. 결과 트리에서 XYData를 두 번 클릭한다. Create XY Data 대화 상자가 나타난다.
2. Operate on XY data를 선택하고 Continue를 클릭한다. Operate on XY Data 대화 상자가 나타난다.
3. Operators 목록에서 differentiate(X)를 클릭한다. differentiate()는 대화 상자의 맨 위에 있는 텍스트 필드에 표시된다.
4. XY Data 필드에서 SWAPPED를 두 번 클릭한다. 산술식 differentiate("SWAPPED")가 텍스트 필드에 표시된다.
5. 커서를 텍스트 필드의 "SWAPPED" 데이터 객체 바로 뒤에 놓고 *5500을 입력하여 스왑된 데이터에 일정한 총 힘 값을 곱한다. differentiate("SWAPPED"*5500)가 텍스트 필드에 표시된다.
6. 대화 상자 아래쪽에 있는 Save As를 클릭하여 미분된 데이터 개체를 저장한다. Save XY Data As 대화 상자가 나타난다.
7. Name 텍스트 필드에 STIFFNESS를 입력하고 OK를 클릭하여 대화 상자를 닫는다.
8. Cancel을 클릭하여 Operate on XY Data 대화 상자를 닫는다.
9. X축과 Y축 라벨이 위 그림과 다르면 그림과 같이 라벨을 사용자 정의한다.
10. 결과 트리에서 XYData 컨테이너 아래의 STIFFNESS를 마우스 버튼 3으로 클릭하고 표시된 메뉴에서 Plot을 선택하고 마운트 변형에 따라 마운트의 축 방향 강성 변화를 나타내는 위 그림의 표시를 표시한다.
마운트의 원형 모양을 표시한다. 원형 모델 모양을 표시하려면 다음과 같이 설정한다.
메뉴에서 Plot → Undeformed Shape를 선택하거나 Visualization 모듈의 도구 상자에 있는 도구를 사용하여 원형 모양을 표시한다(다음 그림 참조).

이 그림이 표시 제목과 겹치고 보기가 어려울 때 도구를 클릭하고 변형 모양에서 마우스 버튼 1을 길게 누른 상태에서 임의 방향으로 이동하여 표시를 이동한다. 또는 표시 제목 표시를 끌 수 있다(Viewport → Viewport Annotation Options).
이 그림에서 축대칭 모델은 평면의 2차원 모양으로 표시된다. 3D 효과는 지정된 각도로 모델을 스윕하여 제공할 수 있다. 또한 선택한 평면(대칭 평면 등)에 관한 결과를 미러링하여 모델의 완전한 3차원 표현에 결과를 렌더링할 수 있다. 이것은 표시 목적이다. 결과의 수치 표현(예: 등고선 범례)은 해석된 모델 부분만 나타낸다. 이 문제에서 대칭 평면은 반드시 글로벌 좌표계면 중 하나와 일치하지 않기 때문에 로컬 좌표계는 미러링 작업을 쉽게 수행할 수 있도록 정의된다.
후처리를 위해 로컬 좌표계를 정의하려면 다음과 같이 설정한다.
1. 메뉴에서 Tools → Coordinate System → Create를 선택한다.
2. Create Coordinate System 대화 상자에서 이름에 rectangular를 입력하고 Continue를 클릭한다.
3. 원점으로 왼쪽 위 모서리에 있는 절점을 X축 상의 점으로, 오른쪽 위 모서리에 있는 절점을 X-Y면의 점으로 왼쪽 아래에 있는 절점을 선택한다.
단면을 미러와 스윕하려면 다음과 같이 설정한다.
1. 메뉴에서 View → ODB Display Options를 선택한다.
2. ODB Display Options 대화 상자에서 Mirror/Pattern 탭을 클릭한다.
3. Mirror CSYS 목록에서 rectangular를 선택한다.
4. 미러 평면으로 XZ를 선택한다.
5. Apply를 클릭한다. 미러 이미지가 표시된다.
6. Sweep/Extrude 탭을 클릭한다.
7. Sweep elements를 켜고 스윕 범위를 0에서 270도로 설정한다. 부분 수를 45로 설정한다.
8. OK를 클릭한다. 스윕 이미지가 표시된다.
고무와 강철을 더 명확하게 구별하려면 요소 특성 지정에 따라 색상을 구분한다.
그다음 변형 후 마운트의 모델 모양을 표시한다. 이러면 변형 후 요소망의 품질을 평가하고 요소망 세분화의 필요성을 결정할 수 있다.
변형 후 모델 모양을 표시하려면 다음과 같이 설정한다.
메뉴에서 Plot → Deformed Shape를 선택하거나 도구를 사용하여 변형 후 마운트의 모델 모양을 표시한다(다음 그림 참조).

강판이 밀어 올려 고무가 양쪽으로 부풀어 오른다. View Manipulation 툴바의 도구를 사용하여 요소망의 왼쪽 아래 모서리를 확대한다. 마우스 버튼 1을 새 뷰의 첫 번째 모서리를 정의하는 위치에서 누른 다음 길게 누른 상태에서 마우스를 이동하여 표시할 영역(다음 그림)을 둘러싸는 상자를 만들고 마우스 버튼을 놓는다. 또는 메뉴에서 View→Specify를 선택하여 표시를 확대하고 이동할 수 있다.
다음 그림에 표시된 것과 유사하게 표시된다(이 이미지와 이후 이미지에서는 이전에 적용된 스윕과 미러링 작업이 일시적으로 삭제된다).

모델의 이 모서리의 일부 요소는 이 영역의 요소망 분할이 거기에서 발생하는 변형 종류에 부적절하므로 심하게 왜곡되었다. 요소의 모양은 해석을 시작할 때 문제가 되지 않지만, 고무가 바깥쪽으로 부풀어 오르면 심하게 왜곡된다. 특히 코너 요소의 왜곡이 심하다. 하중이 추가로 증가하면 요소의 왜곡은 해석이 중단될 만큼 심해질 수 있다.
모델의 오른쪽 아래 모서리의 변형 요소에서 볼 수 있는 돌 모양의 패턴은 그들이 잠겨 있다는 것을 나타낸다. 이런 요소의 정수압 응력의 윤곽 표시(절점을 공유하는 요소 간에 평균화하지 않음)를 수행하면 인접한 요소 간에 정수압 응력이 크게 변한다는 것을 알 수 있다. 이것은 이런 요소에 체적 잠금이 발생했다는 것을 의미한다. 이 현상은 이미 소성의 비압축성과 관련하여 ‘탄소성 문제에 대한 요소 선택’에서 설명하였다. 이 문제에서 체적 잠금은 과도한 구속으로 발생한다. 강판은 고무에 비해 매우 단단하다. 따라서 고무 요소는 접착 면을 따라 횡 방향으로 변형될 수 없다. 이 요소는 비압축성 요구 사항을 만족해야 하므로 매우 정확하게 구속된 상태이며 잠금이 발생한다. 체적 잠금을 해결하는 해석 기법은 ‘체적 잠금을 줄이는 기술’에서 설명한다.
모델의 최대 평면 내 주응력을 표시한다. 아래에 설명된 절차에 따라 마운트의 실제 변형에 대해 채우기 등고선 표시는 표시 제목을 숨긴다.
최대 주응력의 등고선을 표시하려면 다음과 같이 설정한다.
1. 기본적으로 Abaqus/CAE는 기본 필드 출력 변수로 S, Mises를 표시한다. Field Output 툴바에서 불변량으로 Max. Principal을 선택한다. Abaqus/CAE는 자동으로 현재 표시 상태를 변경하고 최대 평면 내 주응력의 등고선 표시를 변형 모양으로 표시한다.
2. Contour Plot Options 대화 상자를 연다.
3. 균일한 등고선 구간 슬라이더를 8로 끕니다.
4. OK를 클릭하여 등고선을 표시하고 대화 상자를 닫는다. 고무 마운트의 요소만 표시하는 표시 그룹을 만든다.
5. 결과 트리에서 ODB 파일 Mount.odb 아래에 있는 Materials 컨테이너를 확장한다.
6. RUBBER를 마우스 버튼 3으로 클릭하고 표시된 메뉴에서 Replace를 선택하여 현재 표시를 선택한 요소로 바꾼다.
7. 뷰포트의 표시가 변경되고 다음 그림과 같이 고무 장착 요소만 표시된다.
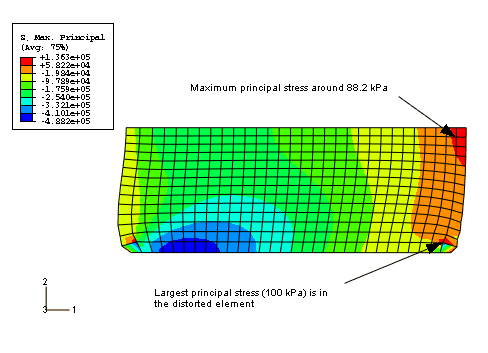
모델의 최대 주응력(윤곽 범례에 표시됨)은 136 kPa이다. 이 모델의 요소망은 상당히 미세하므로 외삽 오차는 최소화되지만, 쿼리 도구를 사용하여 적분점에서 더 정확한 최대 주응력 값을 확인할 수 있다.
적분점의 값을 살펴보면 최대 주응력의 피크 값이 모델의 오른쪽 아랫부분의 왜곡된 요소 중 하나에서 발생한다는 것을 알 수 있다. 이 값은 요소의 왜곡이 크고 체적 잠금이 존재하므로 신뢰할 수 없을 가능성이 크다. 이 값을 무시하면 최대 주응력이 약 88.2 kPa이 되는 영역이 대칭면 근처에 있다.
모델의 주요 변형 범위를 확인하는 가장 쉬운 방법은 등고선 범례에서 최댓값과 최솟값을 표시하는 것이다.
주요 공칭 변형률의 크기를 확인하려면 다음과 같이 설정한다.
1. 메뉴에서 Viewport → Viewport Annotation Options 옵션을 선택한다. Viewport Annotation Options 대화 상자가 나타난다.
2. Legend 탭을 클릭하고 Show min/max values를 선택한다.
3. OK를 클릭한다. 최댓값과 최솟값은 뷰포트의 등고선 범례 아래에 표시된다.
4. Field Output 툴바에서 변수 종류로 Primary를 선택한다(아직 선택하지 않으면). Abaqus/CAE는 자동으로 현재 표시 상태를 변경하고, 최대 평면 내 주응력의 등고선 표시를 변형 모양으로 표시한다.
5. 출력 변수 목록에서 NE을 선택한다.
6. Field Output 툴바의 불변량 목록에서 Max. Principal을 선택한다(아직 선택하지 않으면). 등고선 표시가 변경되고 최대 주 공칭 변형률이 표시된다. 등고선 범례의 최대 주 공칭 변형률에 주목한다.
7. 불변량 목록에서 Min. Principal을 선택한다. 등고선 표시가 변경되고 최소 주 공칭 변형률이 표시된다. 등고선 범례의 최소 주 공칭 변형률에 주목한다.
최대와 최소 주 공칭 변형률은 모델의 최대 인장 공칭 변형률이 약 100%이고 최대 압축 공칭 변형률이 약 56%라는 것을 나타낸다. 모델의 공칭 변형률이 Abaqus의 초탄성 모델이 재료 데이터에 좋은 근사를 제공하는 범위 내에 있으므로, 이 마운트에서 예측된 응답은 재료의 모델링 관점에서 합리적인 것을 확신할 수 있다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 체적 잠금을 줄이는 기술 (0) | 2024.06.01 |
|---|---|
| [Abaqus] 큰 왜곡에 대한 요소망 분할 (0) | 2024.06.01 |
| [Abaqus] 초탄성 해석이란? (1) | 2024.05.31 |
| [Abaqus] 예제: 보강된 판에 대한 폭풍 하중 (0) | 2024.05.31 |
| [Abaqus] 예제: 소성을 고려한 연결용 러그 (0) | 2024.05.31 |




