고정 헤더 영역
상세 컨텐츠
본문
해석 결과가 합리적이라는 첫 번째 기준은 운동 에너지가 내부 에너지와 비교하여 작다는 것이다. 가장 심각한 조건(시험 1)조차도 이 기준이 충족되는 것으로 나타났다. 매끄러운 스텝 시간 변화 곡선을 추가하면 운동 에너지의 진동이 감소하여 만족스러운 준정역학 응답이 얻어졌다.
운동 에너지와 내부 에너지의 시간 이력이 적절하고 합리적이어야 한다는 추가 요구 사항은 매우 효과적이며 필수적이지만 결과 평가는 더 주관적이다. 이런 요구 사항은 성형 공정의 거동에 대해 어느 정도 직관적인 이해가 필요하므로 일반적으로 더 복잡한 성형 공정에 이런 요구 사항을 적용하기는 어렵다.
성형 해석에 준정역학 해가 적당하다는 것이 밝혀졌기 때문에, 다른 몇 가지 주목할 만한 결과를 조사할 수 있다. 다음 그림은 Abaqus/Standard와 Abaqus/Explicit에서 얻은 블랭크의 Mises 응력의 비교이다.
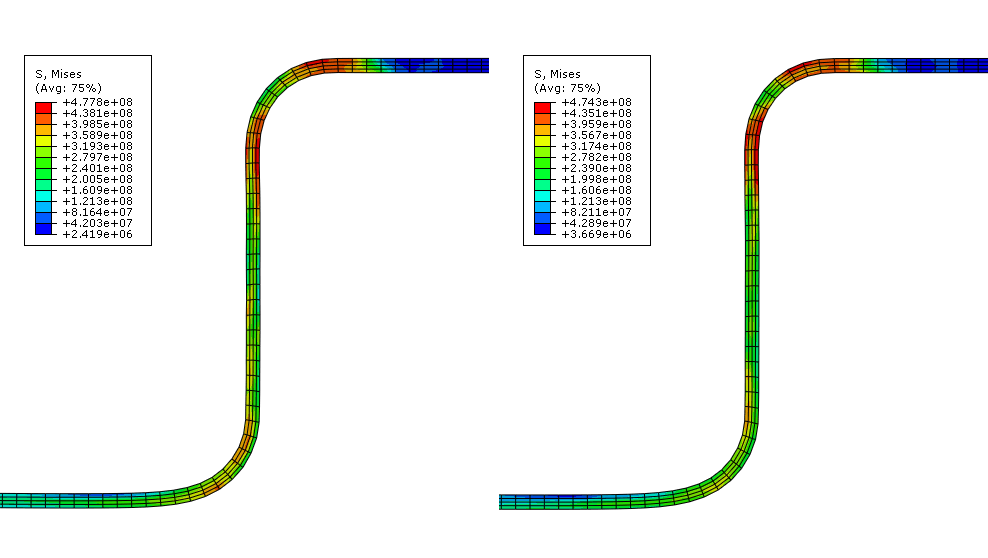
이 표시는 Abaqus/Standard과 Abaqus/Explicit 해석의 각 피크 응력이 서로 1% 이내라는 것을 나타내며 블랭크의 전반적인 응력 등고선이 매우 유사하다는 것을 알 수 있다. 이런 준정역학 해석 결과의 타당성을 추가로 조사하려면, 이들 두 해석의 등가 소성 변형룰의 결과와 최종 변형 형상을 각각 비교해야 한다.
다음 그림은 블랭크의 등가 소성 변형률의 등고선 표시이다.
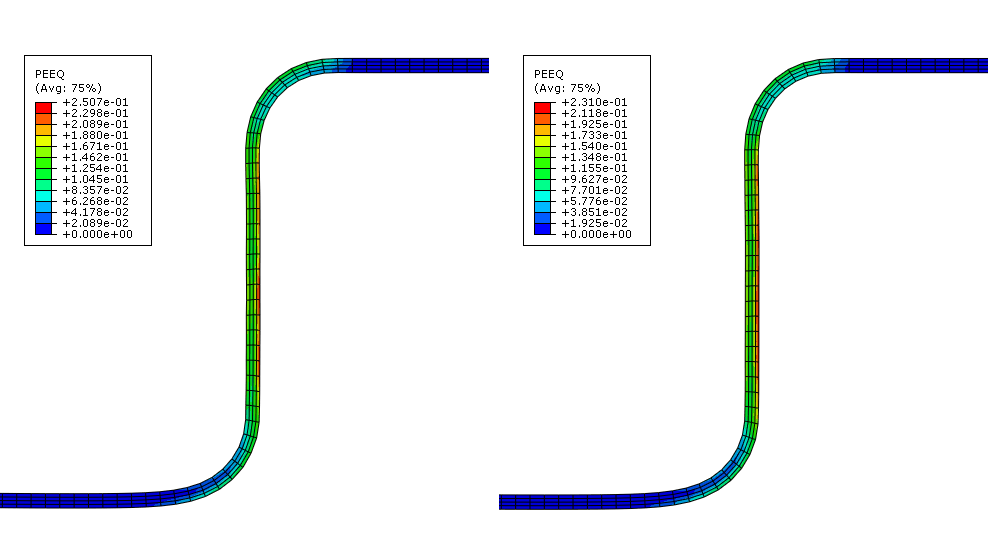
다음 그림은 두 가지 해석으로 예측된 최종 변형 모양이다.
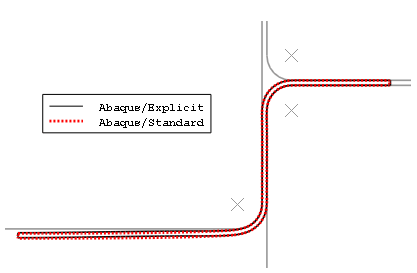
Abaqus/Standard와 Abaqus/Explicit의 해석에 대한 등가 소성 변형률의 결과는 서로 5% 이내이다. 또한 최종 변형 모양의 비교는 외연적 준정역학 해석 결과가 Abaqus/Standard 정역학 해석 결과와 매우 일치한다는 것을 보여준다.
또한 Abaqus/Standard와 Abaqus/Explicit의 해석에서 예측된 정상적인 펀치 힘을 비교해야 한다.
펀치의 힘-변위 기록을 비교하려면 다음과 같이 설정한다.
1. Abaqus/Standard 해석에서 얻은 펀치 변위(U2)와 반력(RF2)의 이력 데이터를 각각 U2-std과 RF2-std로 저장한다.
2. 마찬가지로 Abaqus/Explicit 해석에서 얻은 펀치 변위(U2)와 반력(RF2)의 이력 데이터를 각각 U2-xpl과 RF2-xpl로 저장한다. 그다음 저장된 X-Y 데이터를 계산하여 힘-변위 곡선을 만든다. 힘-변위 표시에서 펀치의 하향 운동이 양의 값을 나타내도록 지정한다. 따라서 힘-변위 곡선을 만들 때 변위 이력 데이터 앞에 음수 기호를 추가한다. 이렇게 하면 음의 두 번째 방향의 움직임이 양수가 된다.
3. 결과 트리에서 XYData를 두 번 클릭한다. 그다음 Create XY Data 대화 상자에서 Operate on XY data를 선택한다. Continue를 클릭한다.
4. Operate on XY data 대화 상자에서 Abaqus/Standard 해석에서 얻은 힘과 변위 이력 데이터를 결합하여 힘-변위 곡선을 만든다. 대화 상자 상단에 산술식이 다음과 같이 표시된다.
combine( -"U2-std", "RF2-std" )
5. Save As를 클릭하여 계산된 변위 곡선을 forceDisp-std로 저장한다.
6. Operate on XY data 대화 상자에서 Abaqus/Explicit 해석에서 얻은 힘과 변위 이력 데이터를 결합하여 힘-변위 곡선을 만든다. 대화 상자 상단에 산술식이 다음과 같이 표시된다.
combine( -"U2-xpl", "RF2-xpl" )
7. Save As를 클릭하여 계산된 변위 곡선을 forceDisp-xpl로 저장한다.
8. 뷰포트에서 forceDisp-std과 forceDisp-xpl을 표시한다.
Abaqus/Standard가 진정한 정적 평형을 풀고 있지만, Abaqus/Explicit는 준정역학 응답을 해석하기 때문에 Abaqus/Explicit의 결과는 Abaqus/Standard의 결과에 비해 노이즈가 꽤 많다. Abaqus/Explicit 이력 데이터의 일부 노이즈는 출력 요청에 지정된 내장된 anti-aliasing 필터로 해석 중에 제거된다. 여기서 Abaqus/CAE의 X-Y 데이터 필터를 사용하여 Abaqus/Explicit의 힘-변위 곡선에서 솔루션의 노이즈를 추가로 제거한다. Abaqus/CAE X-Y 데이터 필터는 시간을 X값으로 사용하는 X-Y 데이터만 적용된다. 이렇게 하면 필터의 컷오프 주파수의 의미를 혼동시키지 않고 필터를 적용하기 전에 내부적으로 수행되는 데이터 조정 문제가 발생하지 않는다. 따라서 forceDisp-xpl을 직접 필터링하는 대신 U2-xpl과 RF2-xpl을 개별적으로 필터링한 다음 결합하여 새로운 힘-변위 곡선을 만든다. 결합된 두 개의 X-Y 데이터 객체는 모두 같은 필터링(해석과 후처리시 모두)을 적용하는 것이 좋다. 이렇게 하면 필터링으로 인한 왜곡(예: 시간 지연)이 결합 데이터에 균일하게 적용된다.
9. Operate on XY data 대화 상자에서 컷오프 주파수가 1100Hz인 Butterworth 필터를 사용하여 힘의 이력 데이터를 필터링한다. 대화 상자 상단에 산술식이 다음과 같이 표시된다.
butterworthFilter(xyData="RF2-xpl",cutoffFrequency=1100)
◉ 필터의 적절한 차단 주파수를 선택하려면 엔지니어링 결정과 모델링을 위한 물리적 시스템에 대한 충분한 이해가 필요하다. 가끔 반복 방법을 사용하여(처음에는 상당히 높은 컷오프 주파수를 사용하고 점진적으로 감소) 물리적 해에 대한 왜곡을 최소화하면서 해의 노이즈 제거할 컷오프 주파수를 찾는다. 적절한 컷오프 주파수를 결정하기 위해 시스템의 고유 진동수에 대한 지식도 도움이 된다. 이 예제의 경우 고유치 추출 해석을 수행하여 변형 전 블랭크의 기본 진동수를 결정했다(140Hz). 그러나 성형 단계가 끝나면 블랭크는 상당한 기본 진동수를 가진다. 최종 모델 배치에서 고유치 추출 해석을 수행하면 성형 단계가 끝날 때 기본 진동수가 약 1,000Hz가 되는 것을 알 수 있다. 따라서 이 모델은 이 값보다 약간 큰 컷오프 주파수를 선택하는 것이 적절하다.
10. Save As를 클릭하여 계산된 변위 곡선을 RF2-xpl-bw1100으로 저장한다.
11. 마찬가지로 컷오프 주파수가 1,100Hz인 Butterworth 필터를 사용하여 변위 이력 데이터를 필터링한다. Operate on XY data 대화 상자의 맨 위에 산술식이 표시된다.
butterworthFilter(xyData="U2-xpl",cutoffFrequency=1100)
12. Save As를 클릭하여 계산된 변위 곡선을 U2-xpl-bw1100으로 저장한다.
13. Abaqus/Explicit의 필터링된 힘과 변위의 시간 기록을 결합한다. Operate on XY data 대화 상자의 맨 위에 산술식이 표시된다.
combine( -"U2-xpl-bw1100", "RF2-xpl-bw1100" )
14. Save As를 클릭하여 계산된 변위 곡선을 forceDisp-xpl-bw1100으로 저장한다.
15. forceDisp-xpl-bw1100을 forceDisp-std과 forceDisp-xpl 표시에 추가한다. 표시 방법을 사용자 정의하고 그림 13.17과 같이 표시한다.
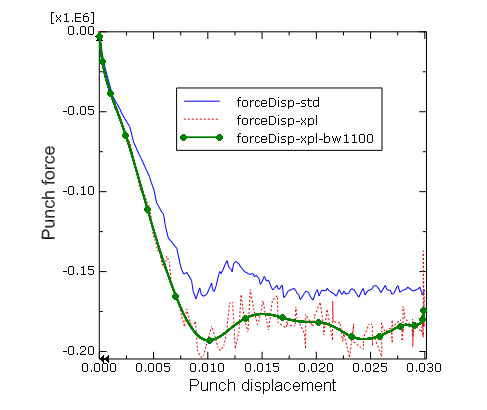
위 그림과 같이 Abaqus/Explicit이 예측한 정상 펀치 힘은 Abaqus/Standard가 예측한 값보다 약 12% 더 크다.
Abaqus/Standard와 Abaqus/Explicit의 결과 차이는 주로 두 가지 요인 때문이다. 첫 번째는 Abaqus/Explicit을 사용하여 재료 데이터를 조정하는 것이다. 두 번째는 이 두 제품 사이의 마찰 효과를 처리하는 방법의 약간의 차이다. Abaqus/Standard는 페널티 방법에 따른 마찰을 사용하는 반면, Abaqus/Explicit는 운동학적 마찰을 사용한다.
이런 비교에서 Abaqus/Standard와 Abaqus/Explicit 모두에서 이런 복잡한 접촉 해석을 처리할 수 있다는 것이 분명하다.
그러나 이 종류의 해석은 Abaqus/Explicit에서 수행할 때 몇 가지 이점이 있다. Abaqus/Explicit는 복잡한 접촉 조건을 더 쉽게 처리할 수 있다. 그러나 준정역학 해석을 위해 Abaqus/Explicit을 선택하면 적절한 하중 속도로 수렴할 때까지 해석을 반복해야 할 수 있다. 하중 속도를 결정할 때는 빠른 하중 속도로 시작하여 필요에 따라 하중 속도를 줄이는 것이 좋다. 이것은 해석 실행 시간을 최적화할 때 효과적이다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] Abaqus/Standard의 스프링백 해석 (0) | 2024.07.10 |
|---|---|
| [Abaqus] 예제: 채널 성형 해석 (4) (0) | 2024.07.10 |
| [Abaqus] 예제: 채널 성형 해석 (2) (0) | 2024.07.10 |
| [Abaqus] 예제: 채널 성형 해석(1) 전처리 (0) | 2024.07.08 |
| [Abaqus] 에너지 균형 (0) | 2024.07.07 |





