고정 헤더 영역
상세 컨텐츠
본문
1) 전처리
다음으로 같은 하중을 순간적으로 주었을 때 러그의 동적 응답을 평가한다. 특히 주목하는 것은 러그의 과도 응답이다. 모델은 Abaqus/Explicit 해석용으로 수정해야 한다. 계속하기 전에 기존 모델을 Explicit이라는 새 모델에 복사한다. 모든 후속 변경은 Explicit 모델에서 수행한다. 혼란을 피하려면 Elastic 모델을 접을 수 있다. 작업을 실행하기 전에 밀도 정의를 재료 모델에 추가하고, 단계 종류를 변경하고, 요소 종류를 변경해야 한다. 또한 필드 출력 요청을 수정해야 한다. 모델을 수정하려면 다음과 같이 설정한다.
1. Steel의 재료 정의를 편집하고 7800의 질량 밀도를 추가한다.
2. 정적 단계 LugLoad를 동적 explicit 단계로 바꾼다. 단계 설명으로 Dynamic lug loading을 입력하고 단계 시간 폭에 0.005초를 입력한다.
3. 필드 출력 요청 F-Output-1를 편집한다. Edit Field Output Request 대화 상자에서 출력을 저장할 등분 시간 간격 수에 125를 입력한다.
4. 기본 기록 출력 요청을 그대로 사용한다.
5. 러그의 요소망 분할에 사용되는 요소 종류를 변경한다. Element Type 대화 상자에서 Explicit 요소 라이브러리, 3D Stress와 Linear 형상 차수를 선택한다. 또한, Hex 형상으로, 강화형 Hourglass 제어를 선택한다. 선택된 요소 타입은 C3D8R이다.
2) 해석
1. 모델 Explicit을 사용하여 작업 expLug를 작성하고 제출한다.
2. 작업 진행 상황을 관찰한다.
expLug Monitor 대화 상자의 맨 위에 해석 진행 상황을 표시한다. 이 표시는 해석을 진행하면서 지속해서 업데이트한다. 해석하면서 발생한 오류와 경고는 해당 탭에 표시된다. 오류가 발생하면 모델을 수정하고 해석을 다시 실행한다. 경고 메시지가 있으면 원인을 조사하고 적절히 조처한다. 앞에서 언급했듯이 일부 경고 메시지는 무시해도 괜찮지만 그렇지 않으면 수정 조치가 필요하다.
3) 후처리
Abaqus/Standard에서 수행한 정역학 해석은 러그 변형, 응력과 변위 출력을 조사했다. Abaqus/Explicit 해석에서 러그 변형, 응력과 변위를 조사할 수 있다. 또한, 순간적으로 작용하는 하중 때문에 과도적인 동적 효과가 발생할 수 있으므로 내부 에너지와 운동 에너지, 변위, Mises 응력의 시간 이력도 조사할 필요가 있다. 이 작업으로 생성된 ODB 파일을 연다.
메뉴에서 Plot → Deformed Shape를 선택하거나 도구 상자의 도구를 사용한다. 그림은 해석이 끝날 때 변형 모양을 보여준다. 앞서 언급했듯이 Abaqus/Explicit에서 기본적으로 대변형 이론이 가정된다. 따라서 변형 배율은 자동으로 1로 설정된다. 변위가 너무 작아 보이지 않으면 스케일링을 사용하여 응답을 쉽게 찾을 수 있다.
러그 진동을 더 쉽게 볼 수 있도록 변형 배율을 50으로 변경한다. 또한 러그 변형의 시간 기록을 애니메이션화하고 시간 기록 애니메이션의 프레임 속도를 줄인다.
러그 변형의 시각 기록 애니메이션은 순간적으로 주어진 하중이 러그에 진동을 일으키는 것을 보여준다. 이런 종류의 하중에서 러그의 거동에 대한 추가 고려 사항은 러그의 운동 에너지, 내부 에너지, 변위와 응력을 시간의 함수로 표시해서 얻을 수 있다.
몇 가지 고려 사항은 다음과 같다.
1. 에너지가 저장되어 있습니까?
2. 이 해석에 대변형 이론이 필요했는가?
3. 피크 응력은 타당한가? 재료는 항복하는가?
X-Y 표시는 변수의 변화를 시간의 함수로 표시할 수 있다. X-Y 표시는 필드 출력과 이력 출력에서 수행할 수 있다.

내부와 운동 에너지를 시간의 함수로 X-Y 표시하려면 다음과 같이 설정한다.
1. 결과 트리에서 expLugODB라는 출력 데이터베이스 아래에 있는 History Output 컨테이너를 확장한다.
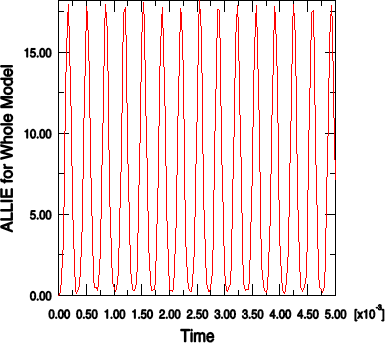
2. 출력 데이터베이스의 이력 영역에 있는 모든 변수의 목록이 표시된다. 표시할 수 있는 이력 출력 변수는 이들뿐이다. 사용할 수 있는 출력 변수 목록에서 ALLIE를 두 번 클릭하여 전체 모델의 내부 에너지를 표시한다.
ODB 파일에서 이 곡선의 데이터를 읽고 그림 4.38과 같은 그래프를 표시한다.
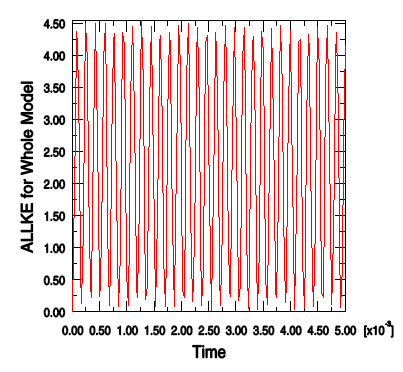
3. 이 작업을 반복하여 전체 모델의 운동 에너지 ALLKE를 표시한다(그림 참고).
내부 에너지와 운동 에너지 모두 러그의 진동을 반영한 진동을 나타낸다. 전체 해석을 통해 운동 에너지는 내부(변형) 에너지로 변환되고 내부 에너지는 운동 에너지로 변환된다. 재료가 선형 탄성이기 때문에 총에너지가 보존된다. 이것은 시스템의 모든 에너지인 ETOTAL을 ALLIE과 ALLKE와 함께 표시하여 확인할 수 있다. ETOTAL의 값은 해석 실행 중 전체 동안 거의 ‘0’으로 유지된다.
러그의 구멍 아래에서 절점 변위를 조사하고 이 해석에서 기하학적 비선형성의 효과의 중요성을 평가한다. 변위 vs. 시간을 표시하려면 다음과 같이 설정한다.
1. 러그 변형을 표시한다. 결과 트리에서 XY Data를 두 번 클릭한다.
2. Create XY Data 대화 상자가 나타나면 ODB field output을 소스로 선택하고 Continue를 클릭한다.
3. XY Data from ODB Field Output 대화 상자가 나타나면 X-Y 데이터를 읽을 위치의 종류로 Unique Nodal을 선택한다.
4. U: Spatial displacement 옆의 화살표를 클릭하여 X-Y 데이터의 변위 변수로 U2를 켠다.
5. Elements/Nodes 탭을 선택한다. X-Y 데이터를 검색할 절점을 식별하는 선택 방법으로 Pick from viewport를 선택한다.
6. Edit Selection을 클릭한다. 뷰포트에서 아래 그림과 같이 구멍 아래에 있는 절점 중 하나를 선택한다(필요한 경우 선택하기 쉽다.)(예: 렌더링 스타일 변경). 프롬프트에서 Done을 클릭한다.
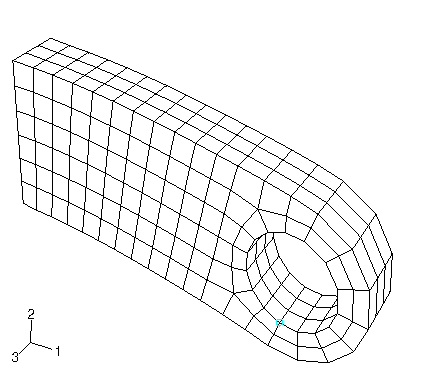
7. XY Data from ODB Field Output 대화 상자에서 Plot을 클릭하여 절점 변위를 시간 함수로 표시한다.
다음 그림과 같이 이 진동 이력은 변위가(구조물의 치수에 비해) 작다는 것을 보여준다.
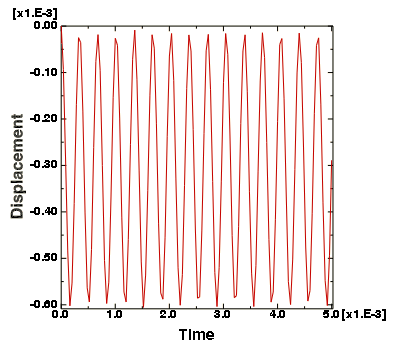
따라서 이 문제는 미소 변형 이론을 사용해도 충분히 풀 수 있다. 미소 변형 이론을 사용하면 해석 결과는 거의 변하지 않고, 이 해석의 계산량은 감소한다.
연결용 러그의 응력의 시간 이력도 조사한다. 러그의 고정단 부근의 영역은 피크 응력의 발생이 예측되고 재료가 항복할 수 있으므로 특히 주목한다. Mises 응력 vs. 시간을 표시하려면 다음과 같이 설정한다.
1. 러그의 변형을 다시 표시한다.
2. XY Data from ODB Field Output 대화 상자에서 Variables 탭을 선택한다. X-Y 데이터 표시 변수에서 U2의 선택을 취소한다.
3. Position 필드를 Integration Point로 변경한다.
4. S: Stress components 옆의 화살표를 클릭하여 X-Y 데이터의 응력 변수로 Mises를 켠다.
5. Elements/Nodes 탭을 선택한다. X-Y 데이터를 검색할 요소를 식별하는 선택 방법으로 Pick from viewport를 선택한다.
6. Edit Selection을 클릭한다. 뷰포트에서 다음 그림과 같이 러그의 고정 가장자리 근처의 요소 중 하나를 선택한다. 프롬프트에서 Done을 클릭한다.

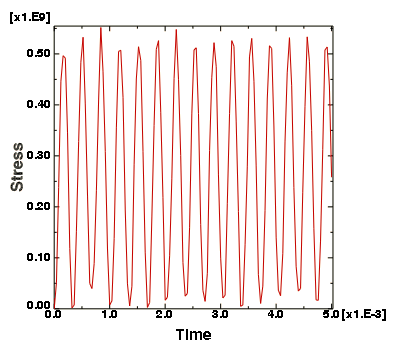
7. XY Data from ODB Field Output 대화 상자에서 Plot을 클릭하여 선택한 요소의 Mises 응력을 시간 함수로 표시한다.
다음 그림과 같이 피크 Mises 응력은 약 550MPa이다. 이 값은 강철의 일반적인 항복 응력보다 크다. 따라서 이 물체는 큰 응력 상태가 발생하기 전에 항복한다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] Shell 요소란 무엇인가? (0) | 2024.05.14 |
|---|---|
| [Abaqus] 요소망의 수렴성에 관하여... (0) | 2024.05.13 |
| [Abaqus] 예제: 연결용 러그 (Abaqus/Standard) (0) | 2024.05.13 |
| [Abaqus] 연속체 요소 사용 (0) | 2024.05.13 |
| [Abaqus] 예제: 해석 출력 결과 표시 (0) | 2024.05.13 |





