2024. 5. 27. 13:09ㆍ공학/유한요소해석
이 예제는 ‘Shell 요소 사용’에서 설명한 선형 경사 플레이트 해석의 연속이며, 다음 그림에 개요를 보여준다. 여기서 Abaqus/Standard로 이 플레이트를 다시 해석하고 기하 비선형성의 효과를 고려한다. 이 해석 결과는 기하 비선형성 효과의 중요성을 결정하고, 결과 선형 해석 결과의 타당성을 결정할 수 있다. 관심이 있다면 이 예제의 끝에 있는 지침에 따라 해석을 확장하고 Abaqus/Explicit을 사용하여 동역학으로 해석할 수 있다.
모델 데이터베이스 파일 SkewPlate.cae를 연다. Linear 모델을 Nonlinear 모델에 복사한다. 비선형 경사판 모델은 기하 비선형 효과를 포함하여 출력 요청을 변경한다.
모델 트리에서 Steps 컨테이너 아래에 있는 Apply Pressure 단계를 두 번 클릭하여 단계 정의를 편집한다. Edit Step 대화 상자의 Basic 탭에서 Nlgeom을 선택한다. 기하 비선형성 효과를 포함하여 단계의 시간 폭을 1.0으로 설정한다. Incrementation 탭에서 초기 시간 증분 값을 0.1로 설정한다. 기본 최대 증분 수는 100이다. Abaqus는 이 상한선보다 적은 수의 증분을 사용할 수 있다. 더 많은 증분이 필요하면 해석이 중단된다. 필요한 경우 비선형 해석 단계로 변경한 것에 따라 단계 설명을 변경한다.
선형 해석에서 Abaqus는 평형 방정식을 한 번만 풀고 이 해법에 관한 결과를 계산한다. 비선형 해석은 각 수렴 증가의 끝에서 결과를 요구하므로 훨씬 더 많은 출력이 생성될 수 있다. 출력 요청을 신중하게 선택하지 않으면 출력 파일이 너무 커지고 때에 따라 컴퓨터의 디스크 공간이 부족하다.
Field Output Requests Manager를 연다. 대화 상자의 오른쪽에 있는 Edit를 클릭하여 필드 출력 요청 편집 대화 상자를 엽니다. 선형 해석 모델에서 정의한 필드 출력 요청을 삭제하고, Output Variables 아래의 Preselected defaults를 선택하여 기본 필드 출력 요청을 지정한다. 이 사전 선택된 출력 변수 세트는 일반 정적 절차에 가장 많이 사용되는 필드 변수 세트이다.
ODB 파일의 크기를 줄이기 위해 두 증가마다 필드를 출력한다. 최종 결과만 관심이 있다면 Last increment를 선택하거나 출력을 저장하는 빈도에 큰 값을 설정할 수 있다. 결과는 지정된 값과 관계없이 항상 각 단계가 끝날 때 저장된다. 따라서 큰 값을 사용하면 최종 결과 만 저장된다.
스팬 중앙 절점의 변위에 대한 이력 출력 요청은 이전 해석을 그대로 사용할 수 있다. 이 결과는 Visualization 모듈의 X-Y 표시 기능을 사용하여 연구한다.
모델 Nonlinear에 대한 작업 NlSkewPlate를 작성하고 해당 설명에 Nonlinear Elastic Skew Plate를 제공한다. 잊지 않고 모델을 새 모델 데이터베이스 파일에 저장한다. 해석 작업을 제출하고, 해석 진행 상황을 관찰한다. 오류가 발생하면 오류를 수정한다. 경고 메시지가 출력되면 원인을 확인하고 필요한 경우 수정 작업을 수행한다.
다음 그림은 이 비선형 경사판 해석에 대한 Job Monitor의 내용이다.
첫 번째 열은 단계 번호를 나타낸다. 이 예는 단 하나의 단계만 있다. 두 번째 열은 증분 번호를 나타낸다. 여섯 번째 열은 각 증분에서 수렴 솔루션을 얻기 위해 Abaqus/Standard가 필요로 하는 반복 수를 나타낸다. 예를 들어, 증분 1에서 네 번의 반복이 필요하다. 8 번째 열은 완료된 전체 단계 시간을 나타내고, 9번째 열은 증가의 크기($ \Delta T$)를 나타낸다.
이 예는 Abaqus/Standard가 증분 크기를 자동으로 제어하는 것을 알 수 있다. 결과적으로 각 증분에 주어진 하중의 비율이 제어된다. 이 해석에서 Abaqus/Standard는 첫 번째 증분에서 전체 하중의 10%를 적용한다. $ \Delta T_{initial}$을 0.1, 단계 시간에 1.0을 입력했다. Abaqus/Standard는 첫 번째 증분으로 해에 수렴하기 위해 네 번의 반복이 필요했다. 두 번째 증가는 두 번의 반복만 필요하므로 Abaqus/Standard는 다음 증분 크기를 자동으로 50% 늘려서 $ \Delta T = 0.15 $이다. 또한 Abaqus/Standard는 네 번째와 다섯 번째 증분으로 $ \Delta T$가 증가했다. 마지막 증분의 크기는 해석 완료 시간에 맞게 조정된다. 이 예에서 마지막 증가의 크기는 0.0875이다.
1) 작업 진단
해석 작업의 진행 상황을 관찰하는 것 외에도 Abaqus/CAE는 필요에 따라 작업의 수렴 거동을 이해하고 모델을 디버깅하는 데 도움이 되는 시각적 진단 도구를 제공한다. Abaqus/Standard는 해석 단계, 증분, 시도와 반복에 대한 정보를 출력 데이터베이스에 저장한다. 이 진단 정보는 작업이 실행될 때마다 자동으로 저장된다. 해석이 예상보다 오래 걸리거나 반대로 빨리 종료되는 경우 Abaqus/CAE에서 작업 진단 정보를 표시하여 원인을 조사하고, 모델 수정 방법을 식별하는 데 도움이 될 수 있다.
Visualization 모듈을 시작하고 ODB 파일 NlSkewPlate.odb를 열고 수렴 기록을 확인한다. 메뉴에서 Tools → Job Diagnostics를 선택하여 Job Diagnostics 대화 상자를 연다. Job History 목록에서 ‘+’ 기호를 클릭하여 목록을 확장하여 해석 작업의 단계, 증분, 시도와 반복을 표시한다. 예를 들어, 다음 그림과 같이 Increment 1에서 Attempt 1을 선택한다.
대화 상자의 오른쪽에 표시되는 Attempt 정보는 증분 크기와 같은 기본 정보가 포함된다. Iterations 정보는 시도한 반복 수가 포함된다. 이 Attempt의 Iteration 1을 선택하여 첫 번째 반복에 대한 자세한 정보를 표시한다. Summary 탭의 정보에서 이 반복이 수렴하지 않은 것을 알 수 있으므로 Residuals 탭을 클릭하여 원인을 확인한다.
다음 그림과 같이 Residuals 탭에는 모델의 평균 힘($ q^{\alpha}$)과 시간 평균 힘( $ q^{- \alpha}$ )의 값이 표시된다.
또한 최대 잔류 힘($ r^{\alpha}_{max} $), 최대 변위 증분($ \Delta u_{\alpha} $), 최대 변위 보정량($ c_{\alpha} $)과 이들이 발생하는 절점과 자유도(DOF)가 표시된다. 이런 발생 위치의 모델 위치는 대화 상자의 아래에 있는 뷰포트 내에서 Highlight selection in viewport를 켠다. 진단 기준의 선택은 계속 유지된다. 즉, 대화 상자의 왼쪽에서 반복 목록의 각 항목을 클릭하면 선택한 기준과 관련된 위치가 반복 기록 내에서 어떻게 변경되는지 빠르게 확인할 수 있다. 이것은 크고 복잡한 모델을 디버깅할 때 매우 유용할 수 있다. 회전 자유도에서도 비슷한 표시를 할 수 있다(Variables 목록 아래에서 Rotation 선택).
이 예에서 단계 정의에서 지정한 것처럼 초기 시간 증분은 0.1이다. 이 증가의 평균 힘은 12.2N이다. 이 증가는 첫 번째 증가이므로 시간 평균 힘($ q^{-\alpha} $)도 같은 값이다. 모델의 최대 잔류 힘($ r^{\alpha}_{max} $)은 -749.6 N이다. 이것은 0.005×$ q^{-\alpha}$보다 분명히 크다. 절점 167의 자유도 1에서 발생했다(실제 값과 절점 번호와 다를 수 있다). 이 모델은 Shell 요소가 포함되었으므로 Abaqus/Standard는 모델의 모멘트 평형을 확인한다. 모멘트/회전의 필드도 평형 검사를 만족시키는 데 실패했다.
평형 검사가 만족하지 않기 때문에 Abaqus/Standard는 새로운 반복을 수행하지만, 변위 수정량을 조사하는 것이 좋다. 첫 번째 단계의 첫 번째 증분의 첫 번째 반복에서 최대 변위 증분($ \Delta u^{\alpha}_{max} $)과 최대 변위 수정량($ c^{\alpha}_{max} $)은 모두 -5.578×10-3m이다. 또한 최대 회전 증분과 최대 회전 보정량은 모두 -1.598×10-2rad이다. 첫 번째 단계의 첫 번째 증분의 첫 번째 반복에서 증분 값과 수정값은 항상 같으므로 절점 변수에 대한 최대 수정량이 최대 증분 값의 1% 미만인지 확인하는 것은 항상 실패한다. 그러나 Abaqus/Standard는 해가 선형이라고 판단하면(잔류의 크기를 기반으로 결정, $ r^{\alpha}_{max} $<10-8 $ q^{- \alpha}$) 이 기준을 무시한다.
Abaqus/Standard는 첫 번째 반복에서 평형 해를 찾지 못했기 때문에 두 번째 반복을 수행한다. 두 번째 반복에서 잔류 정보는 다음 그림에 나와 있다.
두 번째 반복 $ r^{\alpha}_{max} $에서 절점 167의 자유도 1에서 –0.173N으로 떨어진다. 그러나 0.005 × $ q^{- \alpha}$(여기서 $ q^{- \alpha}$=1.00N)는 보다 여전히 작아서 이 반복에서 평형은 만족하지 않는다. $ c^{\alpha}_{max}$=-7.055×10-5(절점 5의 자유도 1에서 발생)는 $ \Delta u^{\alpha}_{max} $=-5.584×10-3(최대 변위 증분)의 1%보다 절댓값이 크기 때문에 변위 수정량의 기준도 아직 만족하지 않는다.
잔류 모멘트의 검사와 최대 회전 보정량의 검사는 둘 다 이 두 번째 반복에서 만족하였다. 그러나 이 해는 잔류 힘 검사(또는 최대 변위 보정 기준)를 통과하지 못했기 때문에 Abaqus/Standard는 반복을 두 번 수행한다. 첫 번째 증분에서 해를 얻는 데 필요한 추가 반복 잔류 정보는 다음 두 그림에 나와 있다.
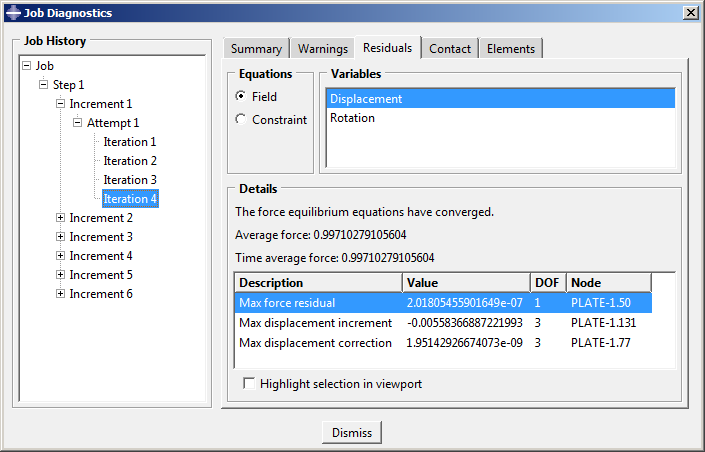
네 번째 반복 후 $q^{- \alpha} = 0.997N$과 절점 76의 자유도 1에서 $ r^{\alpha}_{max} $=1.794×10-7N을 얻는다. 이 값은 $ r^{\alpha}_{max} $<0.005× $ q^{- \alpha} $를 만족하므로 잔류 힘 검사는 통과하고, 최대 변위 증분 $ c^{\alpha}_{max}$와 비교하면 변위 보정량이 필요한 허용치보다 작다는 것을 알 수 있다. 따라서 이런 힘과 변위에 대한 해는 수렴한다. 잔류 모멘트와 회전 보정량 모두에 대한 검사는 두 번째 반복과 마찬가지로 계속 만족한다. 모든 변수(이 예에서는 변위와 회전)에서 평형을 만족시키는 해가 얻어지므로 첫 번째 하중 증가는 완료되었다. Attempt Summary는 이 증가에 필요한 반복 수와 증가 크기를 표시한다.
Abaqus/Standard는 이 하중 증분을 적용하고 해를 구하는 반복 작업을 전체 해석이 완료될 때까지 (또는 지정된 최대 증분에 도달할 때까지) 계속한다. 이 해석은 5번의 증분이 필요하다. 이 단계의 요약은 다음 그림에 나와 있다.
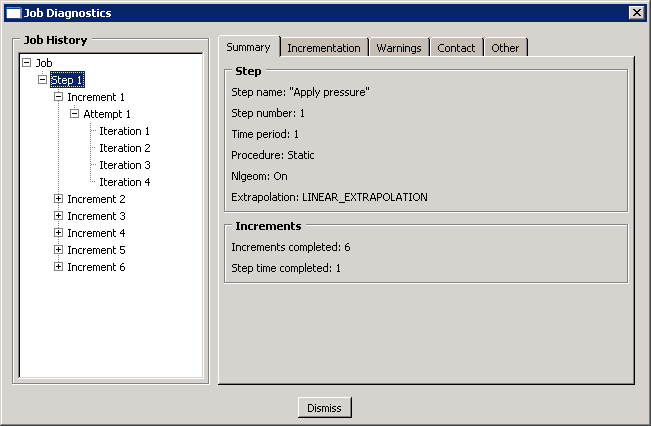
앞의 잔류 정보 외에도 수치 특이성, 제로 피벗과 음의 고유치 각각과 관련된 해석 경고 메시지가 있는 경우 Job Diagnostics 대화 상자(Warnings 탭)가 표시된다. 이런 경고는 항상 원인을 조사해야 한다.
2) 후처리
그다음 결과를 후처리한다. 우선, 유효한 출력 프레임(결과가 출력 데이터베이스에 기록된 증분)을 찾는다. 유효한 프레임을 보려면 다음과 같이 설정한다.
1. 메뉴에서 Result → Step/Frame을 선택한다. Step/Frame 대화 상자가 나타난다.
Abaqus/Standard는 해석 중에 요청된 대로 2 증가마다 필드 출력 결과를 ODB 파일에 기록한다. 다음 그림과 같이 Abaqus/Viewer는 유효한 프레임 목록을 표시한다.
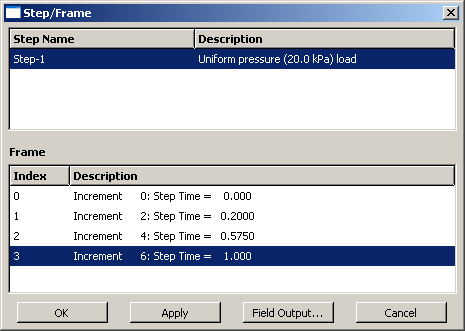
적절한 프레임을 선택하면 ODB 파일에 저장된 다른 증분의 결과를 평가할 수 있다.
새 프레임을 선택하려면 다음과 같이 설정한다.
1. 메뉴에서 Result → Step/Frame을 선택한다. Step/Frame 대화 상자가 나타난다.
2. Frame 메뉴에서 Increment 4를 선택한다.
3. OK를 클릭하여 변경 사항을 적용하고 Step/Frame 대화 상자를 닫는다.
이 상태에서 표시를 수행하면 증분 4의 결과가 사용된다. 이 작업을 관심 있는 증분 번호로 바꾸고 반복하여 ODB 파일의 프레임을 이동한다.
⊙ 다른 방법으로 Frame Selector 대화 상자를 사용하여 결과 프레임을 선택할 수 있다.
스팬 중앙 절점(절점 세트 Midspan)의 변위는 ODB 파일 NlSkewPlate.odb의 이력 영역에 해석 증분에 저장되었다. 이 결과를 사용하여 X-Y 표시를 수행할 수 있다. 특히, 판의 스팬 중앙 가장자리에 있는 절점의 수직 변위의 이력을 표시한다.
스팬 중앙 변위의 X–Y 표시를 수행하려면 다음과 같이 설정한다.
1. 먼저 절점 세트 Midspan에 포함된 절점만 표시한다. 결과 트리에서 ODB 파일 NlSkewPlate.odb 아래에 있는 Node Sets 컨테이너를 확장한다. 세트 MIDSPAN 마우스 버튼 3을 클릭하고, 표시된 메뉴에서 Replace를 선택한다.
2. 어떤 절점이 판의 스팬 중앙 가장자리에 있는지 확인하려면 Common Plot Options 대화 상자를 사용하여 절점 레이블(즉, 번호)을 표시한다.
3. 결과 트리에서 ODB 파일 NlSkewPlate.odb의 History Output 컨테이너를 확장한다.
4. Spatial displacement: U3 at Node xxx in NSET MIDSPAN의 레이블이 있는 출력의 위치를 확인한다. 이 곡선은 스팬의 중앙에 있는 절점 중 하나의 수직 운동을 각각 나타낸다.
5. 스팬 가운데 가장자리에 있는 두 절점의 수직 운동을 선택한다([Ctrl]+클릭 사용). 선택해야 하는 곡선을 결정하려면 절점 레이블을 사용한다.
6. 마우스 버튼 3을 클릭하고, 표시된 메뉴에서 표시를 선택한다. ODB 파일에서 두 곡선의 데이터를 읽고 그림에 표시된 그래프를 표시한다. (편의를 위해 두 번째 곡선은 점선으로 변경되었다. 또한 기본 그리드와 범례의 위치도 변경되었다.)
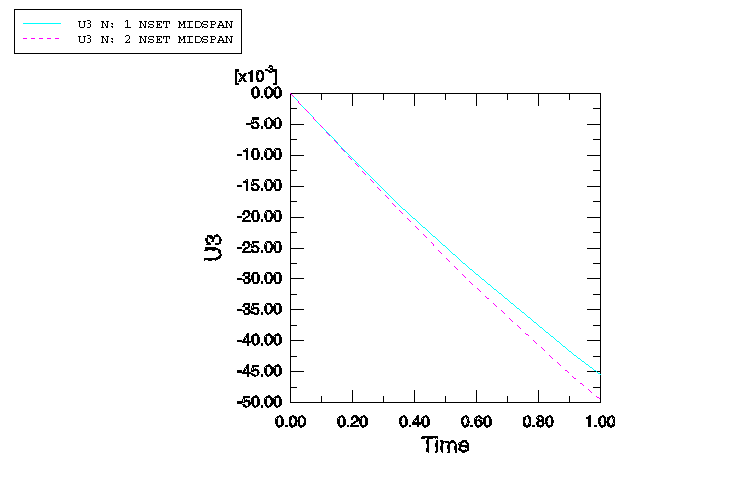
이 해석의 비선형 특성은 이 곡선에 명확하게 나타난다: 즉, 해석이 진행되면서 판이 단단해지고 있다는 것을 알 수 있다. 이 해석에서 변형에 따른 판 강성의 증가는 Membrane 효과 때문이다. 따라서 결과의 피크 변위는 선형 해석에서 예측된 값(기하 비선형성 효과가 포함되지 않은 값)보다 작다.
ODB 파일에 저장된 이력 또는 필드 데이터에서 X-Y 곡선을 만들 수 있다. X-Y 곡선은 외부 파일에서 읽거나 Visualization 모듈에서 대화식으로 입력할 수 있다. 생성된 곡선은 나중에 해당 데이터를 조작하거나 그래프 모양으로 화면에 표시할 수 있다.
스팬 가운데 변위에 대한 표 형식 보고서를 만든다. 절점 세트 Midspan을 사용하여 적절한 표시 그룹을 만들고, 프레임 선택기를 사용하여 최종 프레임을 선택한다. 이 보고서의 내용은 아래와 같다.
이것은 ‘Shell 요소 사용’의 선형 해석에서 변위와 비교한다. 이 해석에서 스팬 중심의 최대 변위는 선형 해석에서 예측된 값보다 약 9% 작다. 이 해석에서 기하 비선형 효과를 고려하면 판의 스팬 중앙의 수직 편향(U3)을 줄일 수 있다.
이 두 해석의 또 다른 점은 비선형 해석의 첫 번째 방향과 두 번째 방향의 ‘0’이 아닌 처짐이다. 어떤 효과가 비선형 해석에서 면내 변위 U1과 U2는 ‘0’이 아닌가? 왜 비선형 해석에서 판의 수직 처짐이 작을까?
이 판은 곡선 모양으로 변형된다. 이것은 비선형 해석에서 고려되는 형상 변화이다. 결과적으로 막 효과는 휨만이 아니라 막 효과에서도 하중 일부를 유지한다. 이것은 판을 단단하게 만든다. 또한 압력 하중(판의 표면에 항상 수직)이 판의 변형에 따라 1방향과 2방향의 성분을 갖기 시작한다. 비선형 해석은 이 경화 효과와 압력 방향의 변화를 고려한다. 선형 해석에서 이런 효과 중 어느 것도 고려되지 않는다.
선형 해석과 비선형 해석의 결과 차이로부터, 이 하중 조건에서 이 판을 해석하려면 선형 해석이 불충분하다는 것을 알 수 있다.
3) Abaqus/Explicit에서 해석 실행
선택적인 연습으로 모델을 수정하고 경사판의 동역학 해석을 Abaqus/Explicit에서 수행할 수 있다. 이렇게 하려면 7,800kg/m<sup>3</sup>의 질량 밀도를 재료 정의에 추가하고, 기존 단계를 외연적 동적 단계로 바꾸고, 요소 라이브러리를 Explicit로 변경한다. 적절한 모델을 변경한 후 새로운 작업을 만들고 실행하여 하중이 순간적으로 가해지는 조건에서 판의 과도 동적 효과를 조사할 수 있다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 외연적 동적 유한요소법 (0) | 2024.05.28 |
|---|---|
| [Abaqus] 비선형 외연적 동역학 해석 (0) | 2024.05.28 |
| [Abaqus] Abaqus 해석에서 비선형성 고려 (0) | 2024.05.27 |
| [Abaqus] 비선형 문제의 해결 (0) | 2024.05.27 |
| [Abaqus] 비선형 해석의 원인 (0) | 2024.05.27 |