2024. 5. 31. 22:35ㆍ공학/유한요소해석
이전 예제에서 비선형 재료 응답을 포함하는 문제를 내연적 방법을 사용하여 해결할 때 발생할 수 있는 수렴 문제를 설명했다. 여기서는 소성을 포함하는 문제를 외연적 동적해석을 사용하여 해결하는 방법을 설명한다. 외연적인 방법은 반복이 필요하지 않으므로 여기서 수렴성은 문제가 되지 않는다.
이 예제에서 보강된 정사각형 판이 폭발 하중을 받았을 때 응답을 Abaqus/Explicit로 평가한다. 이 판은 4개의 모든 측면이 단단히 고정되고, 3개의 같은 간격으로 보강재가 용접된다. 이 판은 25 mm 두께의 강철로 만들어졌으며, 2 m 정사각형이다. 보강재는 두께 12.5 mm의 판으로 100 mm 깊이를 가진다. 다음 그림은 이 판의 모양과 재료 특성의 세부 사항을 보여준다. 이 판은 두께가 다른 전체 치수보다 훨씬 작아서 Shell 요소를 사용하여 만들 수 있다.

이 예제의 목적은 판의 응답을 얻고, 재료 모델이 상세해지면 판의 응답이 어떻게 변하는지 확인하는 것이다. 먼저 표준 탄성 재료 모델의 거동을 해석한다. 그 후, 재료 감쇠와 속도 의존 재료 특성을 고려할 때 영향을 조사한다.
1) 전처리
돌출 Shell의 기본 모양으로 3차원 변형체 파트를 작성하여 판을 만든다. 파트의 근사 크기에 5.0을 사용하고, 파트에 Plate라는 이름을 입력한다. 다음 그림에 표시된 부분 형상을 만드는 권장 방법의 요약은 다음과 같다.

보강된 판의 형상을 작성하려면 다음과 같이 설정한다.
1. 판의 모양을 정의하려면 Create Lines: Connected 도구를 사용하여 모든 수평선을 하나 스케치한다.
2. 보강재 형상을 정의하려면 판에서 위쪽으로 뻗어있는 세 개의 수직선을 추가한다. 이 선의 수평 위치는 이 단계에서 선택 사항이다. 하지만 끝점은 수평선에 있어야 한다.
3. 세 개의 수직선이 같은 길이가 되도록 구속하고, 그중 하나에 길이 0.1m의 치수를 써넣는다.
4. 판을 보강재와 교차하는 위치에서 나눈다.
5. 판의 양쪽 끝 사이의 수평 거리에 치수를 입력하고, 그 값을 2.0 m로 설정한다.
6. 선의 네 개의 수평 부분에 길이 구속을 제공한다. 최종 파트의 스케치는 위 그림에 나와 있다.
7. 스케치를 깊이 2.0 m까지 밀어내고 판을 만든다.
판과 보강재에 재료와 요소 특성을 정의한다. 질량 밀도가 7,800 kg/m³, 영률이 210.0E9 Pa, 푸아송의 비가 0.3인 재료 Steel을 만든다. 이 단계에서 소성 변형이 일어나는지 확실하지 않다. 하지만 이 강철의 항복 응력과 항복 후 거동에 대한 자세한 내용은 알 수 있다. 여기서 이 정보는 재료 정의에 포함된다. 초기 항복 응력은 300 MPa이다. 항복 응력은 35% 소성 변형할 때 400 MPa로 증가한다. 소성 재료 특성을 정의하려면 다음 항복 응력과 소성 변형 데이터를 입력한다.
소성 응력-변형률 곡선은 다음 그림에 나와 있다.

해석 중에 Abaqus는 항복 응력을 현재 소성 변형에서 계산한다. 앞에서 설명한 것처럼 검색과 보간법을 사용한 처리는 응력-변형률 데이터가 같은 간격으로 소성 변형이 정의되었을 때 가장 효율적이다. Abaqus/Explicit는 사용자 입력이 그대로 사용되지 않도록 데이터를 자동으로 조정한다. 이 예제에서 Abaqus/Explicit를 사용하여 데이터를 조정하여 0.025의 증분을 가지는 같은 간격으로 15개의 점으로 데이터를 확장한다.
Abaqus/Explicit는 이 재료 데이터를 조정할 수 없을 때 출력되는 오류 메시지를 설명하려면 조정 허용치를 0.001로 설정하고, Edit Material 대화 상자에서 General → Regularization을 선택한다. 다음 표와 같이 데이터 쌍을 추가한다. 테이블에서 마우스 버튼 3을 클릭하고, 나타나는 메뉴에서 Insert Row를 선택하여 행을 추가할 수 있다.
표. 수정된 소성 데이터
| 항복 응력(Pa) | 소성 변형률 |
| 300.0E6 | 0.000 |
| 349.0E6 | 0.001 |
| 350.0E6 | 0.025 |
| 375.0E6 | 0.100 |
| 394.0E6 | 0.200 |
| 400.0E6 | 0.350 |
작은 공차와 사용자 정의 데이터의 작은 간격이 결합하면, 이 재료의 정의를 조정하기는 어렵다. 다음 오류 메시지가 상태 파일(.sta)에 기록되고, 작업 모듈의 Job Monitor 대화 상자에 표시된다.

계속하기 전에 조정 허용치를 기본값(0.03)으로 되돌리고 추가된 데이터 쌍을 삭제한다.
강철 재료의 정의를 참조하는 두 개의 균일한 Shell 요소 특성을 만들고 각각 다른 Shell 두께를 지정한다. 첫 번째 Shell 요소 특성은 Plate_Section이라고 이름을 입력하고 재료에 Steel을 선택하고, Shell thickness 값에 0.025m를 입력한다. 두 번째 Shell 요소 특성은 Stiff_Section이라는 이름을 입력하고, 재료에 Steel을 선택하고, Shell thickness 값에 0.0125m를 입력한다.
Stiff_Section 정의를 모든 보강재에 지정한다. [Shift]+클릭을 사용하여 뷰포트에서 모든 보강재를 선택한다.
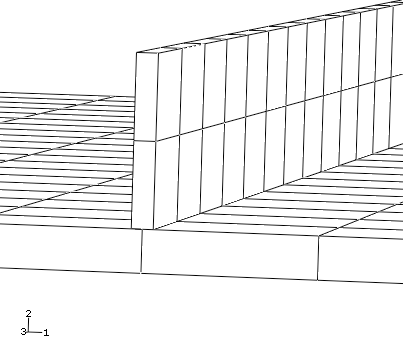
Plate_Section 정의를 판에 지정하기 전에 다음을 고려한다. 판과 보강재가 기본 거동인 중립면에서 직접 결합하면, 다음 그림과 같이 겹치는 영역이 발생한다.

판과 보강재의 두께는 구조물의 전체 치수와 비교하면 매우 작지만, 판의 참조 면을 중립면에서 오프셋 하여 더 정확한 모델을 만들 수 있다. 이 중첩 재료와 중첩으로 생긴 추가 강성은 해석 결과에 거의 영향을 미치지 않는다. 이 기술을 사용하면 보강재를 그림 10.30과 같이 판재와 겹치지 않고 판과 접합할 수 있다.
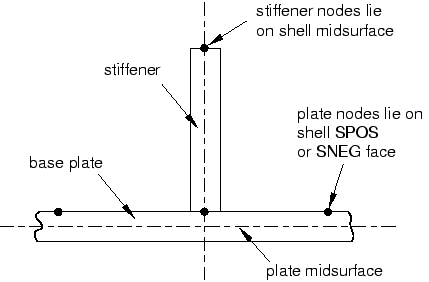
판의 기준면을 SPOS와 SNEG 중 하나로 오프셋 할지 결정하려면 Shell의 법선 방향을 Query하고, 보강재의 어느 쪽을 향하는 판 면의 색을 기록한다(브라운은 정측, 보라색은 부측). 필요하면 판의 모든 부분이 일관된 법선 방향을 갖도록 판의 법선 방향을 반전시킨다(Assign → Element Normal). 다음으로, Plate_Section 정의를 판의 영역에 지정한다. Edit Section Assignment 대화 상자에서 판의 갈색 면이 보강재 쪽을 향하면, Shell 오프셋을 Top surface로 설정하고, 보라색 면이 보강재 쪽을 향하면 Shell 오프셋을 Bottom surface로 설정한다.
오프셋을 확인하려면 View → Part Display Options를 선택한다. Part Display Options 대화 상자에서 Shell 두께를 렌더링하려면 Render Shell thickness를 선택한다. 필요하면 오버랩이 제거되도록 오프셋을 수정한다.
모델은 요소 특성 지정에 따라 색으로 구분되어 특성이 올바르게 지정되었는지 확인할 수 있다. Color Code 툴바에서 Sections을 선택한다.
판의 Independent Instance를 만든다. 기본 직교 좌표계 사용하면 판은 1-3 평면에 있다.
이 시점에서 나중에 경계 조건과 출력 요청을 지정하는 데 사용할 기하 형상 세트를 작성하는 것이 유용하다. 다음 그림과 같이 판의 가장자리에 세트 Edge와 판과 중앙 보강재 교선 중심점의 세트 Center를 작성한다. 세트 Center를 만들려면 먼저 가장자리 Partition Edge: Enter Parameter 도구를 사용하여 원래 파트의 가장자리를 절반으로 나누어야 한다.
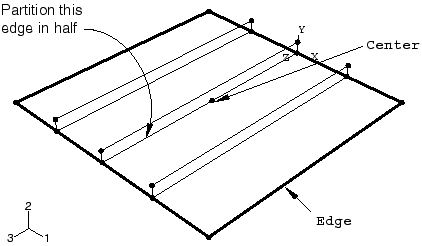
하나의 동적 외연적 단계를 만든다. 단계에 Blast라는 이름을 지정하고 해당 단계의 설명에 Apply blast loading을 지정한다. 단계의 시간 폭에 50E-3초를 입력한다.
일반적으로 해석 중에 내보내는 프레임 수를 제한하여 ODB 파일을 적절한 크기로 유지하는 것이 좋다. 이 해석은 2 ms마다 정보를 저장하여 구조물의 응답을 조사하기에 충분히 상세한 정보를 제공한다. 기본 출력 요청 F-Output-1을 편집하여 사전 선택된 필드 데이터를 단계 안에 저장하는 간격을 25로 설정한다. 이렇게 하면 전체 단계가 50 ms이므로 선택한 데이터가 2 ms마다 기록된다.
모델의 선택한 영역에 대한 보다 자세한 출력은 이력 출력으로 저장할 수 있다. 단계 Blast에 대한 이력 출력 요청 Center-U2를 만든다. 출력 영역에서 Center를 선택하고, 변환 출력 변수로 U2를 선택한다. 해석 중에 출력이 저장되는 간격 수에 500을 입력한다.
그다음 해석에 사용하는 경계 조건을 정의한다. 단계 Blast에 Symmetry/Antisymmetry/Encastre)의 기계적 경계 조건을 만들고, Fix edges라는 이름을 입력한다. 기하 형상 세트 Edge를 사용하여 이 경계 조건을 판의 가장자리에 적용하고, ENCASTRE를 지정하여 세트를 완벽히 구속한다.
판은 시간에 따라 변화하는 하중을 받는다. 하중의 압력은 해석 개시로부터 1 ms 사이에 0에서 최댓값 7.0×105Pa까지 급속히 상승한다. 1 ms에서 10 ms까지 일정하게 유지된다. 그 후, 10 ms에 걸쳐 ‘0’으로 떨어진다. 해석의 나머지 시간은 ‘0’으로 유지한다. 상세한 것은 다음 그림과 같다.
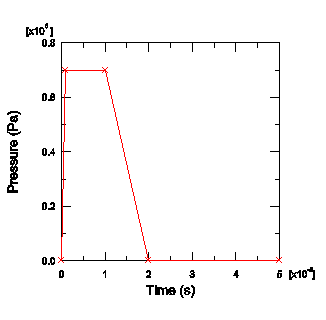
표 형식의 시간 변화 곡선 Blast를 정의한다. 다음 표의 시간 변화 데이터를 입력하고 0.0의 평활화 변수를 지정한다.
표 10.3 폭발 하중의 시간 변화
| 시간 | 시간 변화 |
| 0.0 | 0.0 |
| 1.0E−3 | 7.0E5 |
| 10.0E−3 | 7.0E5 |
| 20.0E−3 | 0.0 |
| 50.0E−3 | 0.0 |
다음으로 압력 하중을 정의한다. 하중의 크기는 시간 변화 곡선으로 정의하므로, 1단위의 압력만을 판에 적용하면 된다. 판의 상면이 밀리는 압력을 작용한다. 보강재는 판의 밑면에 존재한다. 이런 압력 하중은 보강재의 외부 층을 인장 상태로 만든다.
압력 하중을 정의하려면 다음과 같이 설정한다.
1. 모델 트리에서 Loads 컨테이너를 두 번 클릭한다. 나타나는 Create Load 대화 상자에서 하중에 Pressure load라는 이름을 지정하고, 이 하중이 적용하는 단계로 Blast를 선택한다. 하중 카테고리의 Mechanical과 하중 종류에 Pressure를 선택한다. Continue를 클릭한다.
2. 판에 속하는 모든 서피스를 선택한다. 해당 서피스 선택이 끝나면 Done을 클릭한다.
Abaqus/CAE는 서로 다른 두 가지 색상을 사용하여 Shell 표면의 뒷면을 구별하여 표시한다. 하중 정의를 완성하려면 판의 각 면에서 색상을 통합해야 한다.
3. 필요한 경우 프롬프트에서 Flip a surface를 선택하여 판의 색상을 반전시킨다. 판 윗면의 모든 면이 같은 색이 될 때까지 이 작업을 반복한다.
4. 프롬프트에서 보강재가 없는 쪽 판 면의 색상을 선택한다.
5. Edit Load 대화 상자가 나타나면 1.0 Pa의 균일 압력을 입력하고, 시간 변화 곡선 정의 Blast를 선택한다. OK를 클릭하여 하중 정의를 완료한다.
판의 하중과 경계 조건은 다음 그림과 같다.
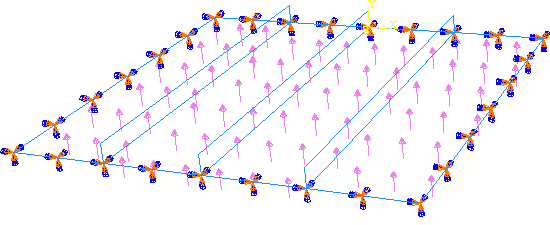
전체 요소 크기가 0.1인 Seed를 파트 Instance에 제공한다. 또한 seed → edge를 선택하고, 각 보강재의 높이 방향으로 두 개의 요소를 만들도록 지정한다. Local Seeds 대화 상자에서 방법으로 By number를 선택하고, 요소 수를 2로 설정하고 선택한 가장자리가 포함된 세트를 만드는 옵션을 켠다. 플레이트와 보강재는 Explicit 요소 라이브러리의 4각형 Shell 요소(S4R)를 사용하여 요소망으로 나눈다. 요소망 분할의 결과는 다음 그림에 나와 있다. 이 비교적 거친 요소망은 계산 시간을 최소화하면서 적당한 정확도를 제공한다.
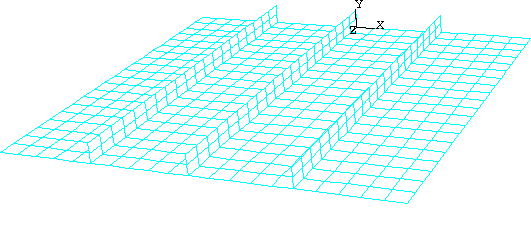
Blast_Load라는 작업을 만든다. 작업 설명에 Blast load on a flat plate with stiffeners:S4R elements(20x20 mesh) Normal stiffeners(20x2)를 지정한다.
모델을 모델 데이터베이스 파일에 저장하고, 해석 작업을 제출한다. 해석 진행 상황을 관찰하고, 모델링 오류가 감지되면 수정하고, 경고 메시지가 있으면 원인을 조사한다.
2) 후처리
작업을 완료하면 Visualization 모듈을 시작하고, 이 작업이 생성한 ODB 파일(BlastLoad.odb)을 연다. 기본적으로 Abaqus는 음영 렌더링 스타일로 원형 모양을 표시한다.
기본 뷰는 등각 투상도이다. 이것은 이 플레이트의 쉬운 보기가 아니다. 뷰를 개선하려면 View 메뉴의 옵션 또는 View Manipulation 툴바의 도구를 사용하여 뷰를 회전한다. 뷰를 지정하고 뷰를 회전시키는 관점의 방법을 선택한다. 시점 벡터의 X, Y, Z 좌표에는 1, 0.5, 1을, 상향 벡터의 좌표에는 0, 1, 0을 입력한다.
후처리할 때 요소 특성 지정과 Shell 두께를 표시할 수 있다. 예를 들어, 공통 요소 특성이 지정된 영역을 색으로 구분하여 특성이 올바르게 지정되었는지 확인할 수 있는 Color Code 툴바에서 Sections를 선택하고 요소 특성 지정에 따라 요소망으로 착색한다. Shell 두께를 렌더링하려면 메뉴에서 View → ODB Display Options를 선택한다. ODB Display Options 대화 상자에서 Shell 두께를 렌더링하려면 Render shell thickness를 선택하고, Apply를 클릭한다. 다음 그림과 같이 모델이 올바르게 표시되면 나머지 후처리 절차로 진행하기 전에 이 옵션을 선택 취소하고 OK를 클릭한다. 모델이 올바르지 않으면 요소 지정을 수정하고, 작업을 다시 실행한다.
앞의 예제에서 언급했듯이 결과를 애니메이션으로 만들면, 폭발 하중이 작용할 때 플레이트의 동적 응답에 대한 전반적인 이해를 얻을 수 있다. 먼저 변형 모양을 표시한다. 그다음 변형 모양의 시간 기록 애니메이션을 만든다. Animation Options 대화 상자를 이용하여 모드를 Play once로 변경한다.
이 애니메이션에서 폭발 하중이 작용하면, 플레이트가 휘어지기 시작하는 것을 알 수 있다. 하중이 작용하는 기간에 플레이트는 진동을 개시하고, 폭발 하중이 ‘0’까지 저하된 이후에도 진동을 계속한다. 최대 변위는 약 8 ms에서 발생한다.
다음 그림에서 그 상태의 변형을 보여준다. 애니메이션 이미지를 나중에 재생하려면 파일에 저장할 수 있다.
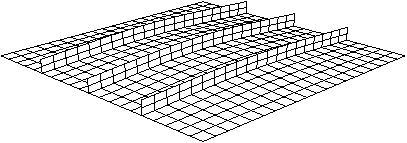
애니메이션을 저장하려면 다음과 같이 설정한다.
1. 메뉴에서 Animate → Save As를 선택한다. Save Image Animation 대화 상자가 나타난다.
2. Settings 필드에 파일 이름 blast_base를 입력한다. 애니메이션 형식은 AVI, QuickTime, VRML 또는 Compressed VRML 중 하나로 지정할 수 있다.
3. QuickTime 형식을 선택하고 OK를 클릭한다.
애니메이션은 자신의 현재 디렉터리에 blast_base.mov로 저장한다. 저장한 애니메이션은 소프트웨어를 사용하여 Abaqus/CAE 외부에서 재생할 수 있다.
변형 형상으로 플레이트의 변형을 조사하는 것은 쉽지 않기 때문에, 중심 절점의 처짐 응답을 그래프의 형태로 표시하는 것이 바람직하다. 플레이트의 중심에 있는 절점에서 최대 처짐이 발생하는 것을 특히 주목한다.
다음 그림과 같이 중심 절점 변위의 시간 기록을 표시한다. 변위 단위는 mm이다.
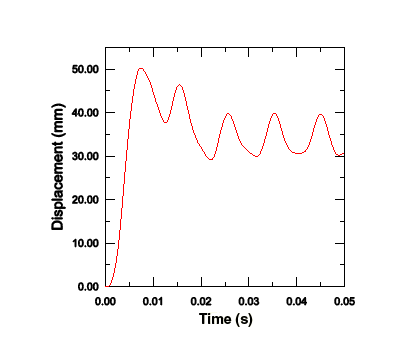
중심 절점 변위의 시간 기록을 표시하려면 다음과 같이 설정한다.
1. 결과 트리에서 플레이트 중앙의 절점인 세트 center에서 이력 출력 데이터 Spatial displacement: U2를 두 번 클릭한다.
2. 현재 X–Y 데이터 저장한다. 결과 트리에서 해당 데이터의 이름을 마우스 버튼 3으로 클릭하고, 표시되는 메뉴에서 Save As를 선택한다. 데이터에 DISP라는 이름을 붙인다. 이 표시의 변위 단위는 m이다. 데이터를 수정하여 변위(단위는 mm) vs. 시간 표시를 새 데이터 객체로 만든다.
3. 결과 트리에서 XYData 컨테이너를 확장한다. DISP 데이터가 아래에 나열된다.
4. 결과 트리에서 XYData를 두 번 클릭한다. 그다음 Create XY Data 대화 상자에서 Operate on XY Data를 선택한다. Continue를 클릭한다.
5. Operate on XY Data 대화 상자에서 DISP에 1000을 곱하여 변위 값을 미터에서 밀리미터로 변환하는 표시를 만든다. 대화 상자 상단에 산술식이 다음과 같이 표시된다.
"DISP" * 1000
6. Plot Expression을 클릭하여 수정된 X-Y 데이터를 확인한다. 이 데이터를 U2_BASE로 저장한다.
7. Operate on XY Data 대화 상자를 닫는다.
8. 도구 상자에서 Axis Options 도구를 클릭한다. Axis Options 대화 상자에서 X축 제목을 Time(s)으로, Y축 제목을 Displacement(mm)로 변경한다. OK를 클릭하여 대화 상자를 닫는다. 그림의 결과는 위 그림과 같다. 이 표시에서 변위는 7.7 ms에서 50.2 mm의 최댓값에 도달하고, 폭발 하중이 제거된 후에 진동하는 것을 알 수 있다.
출력 데이터베이스에 이력 출력으로 저장된 나머지 데이터는 모델의 전체 에너지이다. 이 에너지 이력은 모델의 결함을 식별하거나 심각한 물리적 영향을 밝히는 데 도움이 될 수 있다. 5가지 에너지 출력 변수 ALLAE, ALLIE, ALLKE, ALLPD, ALLSE의 시간 기록을 표시한다.
모델 에너지의 시간 기록을 표시하려면 다음과 같이 설정한다.
1. ALLAE, ALLIE, ALLKE, ALLPD, ALLSE 출력 변수의 이력 출력을 X-Y 데이터로 저장한다. 기본 이름이 각 곡선에 지정된다. 출력 변수 이름 ALLAE, ALLKE 등에 따라 각 이름을 변경한다.
2. 결과 트리에서 XYData 컨테이너를 확장한다. ALLAE, ALLIE, ALLKE, ALLPD, ALLSE의 X-Y 데이터 객체가 아래에 나열된다.
3. [Ctrl]+클릭을 사용하여 ALLAE, ALLIE, ALLKE, ALLPD, ALLSE를 선택한다. 마우스 버튼 3을 클릭하고, 표시된 메뉴에서 표시를 선택하여 이런 에너지 곡선을 표시한다.
4. 이 표시에서 각 곡선을 더 명확하게 구분하려면 Curve Options 대화 상자를 열고 해당 선의 스타일을 변경한다.
º 곡선 ALLSE는 파선 스타일을 선택한다.
º 곡선 ALLPD는 점선 스타일을 선택한다.
º 곡선 ALLAE는 쇄선 스타일을 선택한다.
º 곡선 ALLIE는 두 번째로 가장 얇은 선 종류를 선택한다.
5. 범례의 위치를 변경하려면 Chart Legend Options 대화 상자를 열고, Area 탭으로 전환한다.
6. 이 페이지의 Position 영역에서 Insert를 켜고 Dismiss를 클릭한다. 그림 10.38과 같이 범례를 뷰포트에서 드래그하여 그리드에 범례를 맞춘다.
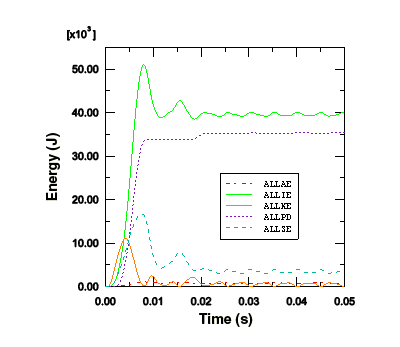
하중이 제거되고 플레이트가 자유롭게 진동하기 시작하면 변형률 에너지의 감소에 따라 운동 에너지가 증가하는 것을 알 수 있다. 플레이트가 최대 처짐에 도달하고 결과적으로 변형률 에너지가 최대가 되면, 플레이트는 거의 완벽히 고정되어 운동 에너지가 최소화한다.
소성 변형률 에너지는 평평한 부분까지 상승한 다음 다시 상승한다. 운동 에너지 표시에서 두 번째 소성 변형률 에너지의 상승은 플레이트가 최대 변위에서 반전한 후 반대 방향으로 이동할 때 발생하는 것으로 나타났다. 따라서 폭발 하중 후 리바운드에서 소성 변형이 발생하는 것을 알 수 있다.
Hourglass 모드가 이 해석에서 문제가 되는 징후는 없지만, 인공 변형률 에너지를 확인하기 위해 이것을 확인한다. ‘연속체 요소 사용’에서와 같이, 인공 변형률 에너지(또는 ‘Hourglass 강성’)는 Hourglass 변형을 억제하는 데 사용되는 에너지이며, 이 에너지의 누적값은 출력 변수 ALLAE로 표시된다. 이 Hourglass 제어에 대한 설명은 Shell 요소도 같이 적용된다. 플레이트가 변형할 때 소성 변형률로 에너지가 분산되므로 전체 내부 에너지는 탄성 변형률 에너지보다 상당히 크다. 따라서 이 해석에서 인공 변형률 에너지를 탄성 변형률 에너지뿐만 아니라 분산 에너지를 포함하는 에너지양과 비교하는 것은 매우 의미가 있다. 후자의 에너지양 변수는 모든 내부 에너지양의 합계인 전체 내부 에너지 ALLIE이다. 인공 변형률 에너지는 전체 내부 에너지의 약 2%이다. 이것은 Hourglass 모드가 문제가 되지 않는다는 것을 나타낸다.
변형 형상으로부터 중앙 보강재가 거의 순수한 면내 휨을 받는다는 것을 알 수 있다. 보강재의 깊이 방향으로 1차 저감 적분 요소를 2개만 사용하므로, 면내 휨 거동의 모델링은 불충분하다. 이 거친 요소망은 Hourglass 모드가 거의 없으므로 적절한 해를 얻는 것처럼 보인다. 하지만 완성하려면 보강재의 요소망을 미세하게 만들 때 해의 변화를 조사한다. 요소망을 세분화하면 요소 수가 증가하고, 요소 크기가 줄어들어 계산 시간이 증가하므로 요소망을 세분화할 때 주의가 필요하다.
요소망을 편집하고 요소망 밀도를 다시 지정한다. 미리 저장된 Edge 세트를 사용하여 각 보강재의 높이 방향으로 4개의 요소를 지정하고, 파트 Instance를 다시 요소망으로 나눈다. 새 작업 Blast_Load_Refined를 만든다. 이 해석 작업을 제출하고, 작업 실행이 완료되면 결과를 확인한다.
이 요소 수의 증가는 계산 시간을 약 20% 증가시킨다. 또한 안정 시간 증분은 보강재의 최소 요소 치수의 감소 결과로 약 절반으로 감소한다. 계산 시간의 전체 증가는 이 두 가지 효과의 조합이므로, 이 미세한 요소망의 계산 시간은 원래 요소망의 계산 시간의 약 1.2×2인 2.4배로 증가한다.
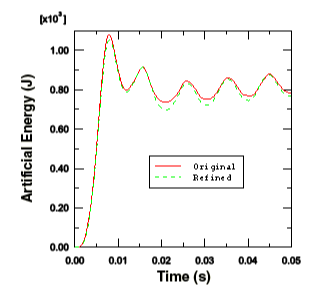
다음 그림은 원래 요소망과 보강재가 미세한 요소망 모두에게 인위적인 에너지의 시간 이력이다. 인공 에너지는 미세한 요소망이 약간 작다. 결과적으로 원래의 요소망을 미세하게 만들어도 해석 결과에 의미 있는 변화가 일어날 것으로 생각되지 않는다.
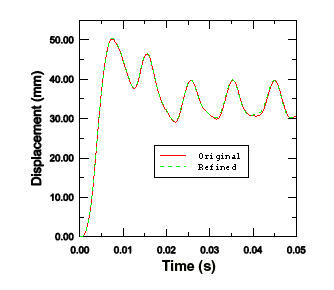
다음 그림에서 플레이트의 중심 절점 변위는 두 경우 모두 거의 같으며, 원래 요소망이 전체 응답을 잘 포착한다는 것을 알 수 있다. 한편, 미세한 요소망의 장점은 보강재 내부의 응력과 소성 변형의 변화가 더 잘 표현한다는 것이다.
이 절에서 Visualization 모듈의 등고선 기능을 사용하여 플레이트의 Mises 응력 분포와 등가 소성 변형률 분포를 표시한다. 보강재의 요소망을 미세하게 만든 모델을 사용하여 표시한다. 메뉴에서 File → Open을 선택하고, 파일 Blast_Load_Refined.odb를 선택한다.
Mises 응력과 등가 소성 변형률의 등고선을 표시하려면 다음과 같이 설정한다.
1. Field Output 툴바의 왼쪽에 변수 종류 목록에서 Primary를 선택한다.
2. 툴바 중앙의 출력 변수 목록에서 S를 선택한다. 응력 불변량과 구성 요소는 오른쪽의 다음 목록에서 선택할 수 있다. Mises 응력 불변량을 선택한다.
3. 메뉴에서 Result → Section Points를 선택한다.
4. Section Points 대화 상자가 나타나면 유효한 위치로 Top and bottom을 선택하고, OK를 클릭한다.
5. Plot → Contours → On Deformed Shape를 선택하거나 도구 상자의 도구를 사용한다.
Abaqus는 각 Shell 요소의 상단과 하단 모두 Mises 응력의 등고선을 그린다. 이 표시를 더 쉽게 보려면 모델을 뷰포트에서 회전시킨다.
이전에 애니메이션 연습에서 설정한 뷰를 응력 분포를 쉽게 볼 수 있도록 변경한다.
6. 뷰 툴바의 도구를 사용하여 뷰를 기본 등각 투상도 뷰로 변경한다.
⊙ Views 툴바가 보이지 않으면 메뉴에서 View → Toolbars → Views를 선택한다.
다음 그림은 해석이 끝날 때 Mises 응력의 등고선 표시이다.
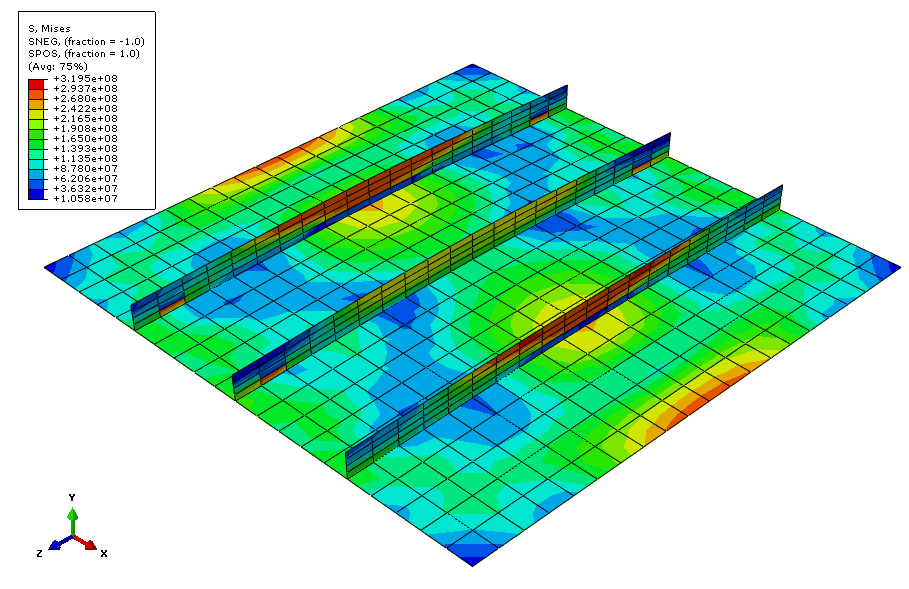
7. 마찬가지로, 등가 소성 변형률의 등고선을 표시한다. Field Output 툴바의 왼쪽에 있는 변수 종류 목록에서 Primary를 선택하고, 다음 출력 변수 목록에서 PEEQ를 선택한다.
다음 그림은 해석이 끝날 때 등가 소성 변형률의 등고선 표시이다.

3) 해석 평가
이 해석의 목적은 폭발 하중을 받는 플레이트의 변형과 다양한 부분의 응력을 조사하는 것이다. 해석의 정확성을 결정하려면 수행된 가정과 근사를 검토하고, 모델에 존재하는 몇 가지 제한 사항을 식별해야 한다.
감쇠가 없는 구조는 일정한 진폭으로 진동을 계속한다. 이 해석의 50 ms 이후에는 진동 주파수가 약 100 Hz가 될 것으로 생각한다. 이런 구조에서 진동은 시간이 지나면서 감소하는 경향이 있으며 5~10회의 진동으로 실제 사라진다. 따라서 진폭이 일정한 진동은 실제로 일어날 것으로 예상되는 응답이 아니다. 일반적으로 에너지 손실은 지지부의 마찰 효과와 공기 감쇠와 같은 다양한 메커니즘으로 발생한다.
따라서 이 에너지 손실을 만들려면 해석에 감쇠를 도입하는 것을 고려해야 한다. 이 해석에서 점성 효과로 분산된 에너지 ALLVD는 ‘0’이 아니며, 감쇠가 이미 존재하는 것을 알 수 있다. 기본적으로 체적 점성(bulk viscosity) 감쇠가 항상 존재하며, 고속 현상 모델링을 개선하려고 도입하였다.
이 Shell 모델은 선형 감쇠만 있다. 기본값에서 진동은 결국 사라진다. 하지만 이 체적 점성 감쇠는 매우 작아서 진동이 사라지는 데 오랜 시간이 걸린다. 더 현실에 가까운 구조 응답을 도입하려면 재료 감쇠를 사용해야 한다. 따라서 재료의 정의를 수정한다.
감쇠를 재료에 추가하려면 다음과 같이 설정한다.
1. 모델 트리에서 Materials 컨테이너 아래의 Steel을 두 번 클릭한다.
2. Edit Material 대화 상자에서 Mechanical → Damping을 선택하고, 질량에 비례하는 감쇠 계수 Alpha에 50을 지정한다. Beta는 강성에 비례하는 감쇠를 제어하는 변수이다. 이 단계는 0으로 둔다.
3. OK를 클릭한다.
플레이트 진동의 지속 시간은 약 30 ms이다. 해석의 시간 폭을 늘려 진동이 감쇠하고, 사라지는 시간을 충분히 확보해야 한다. 단계 정의를 편집하고, 단계 Blast의 시간 폭을 150E-3초로 늘린다.
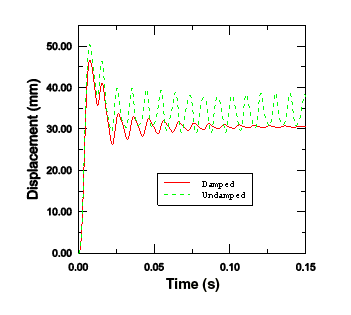
감쇠가 있는 해석의 결과는 질량에 비례하는 감쇠의 효과를 명확하게 보여준다. 다음 그림은 감쇠가 있는 해석과 감쇠가 없는 해석 모두의 중심 절점 변위의 시간 경향이다. 감쇠가 없는 모델의 해석 시간은 데이터를 더욱 효과적으로 비교하려면 150 ms로 연장한다. 피크 응답도 감쇠로 감소한다. 감쇠가 있는 해석은 해석이 끝날 때까지 진동이 거의 정적 상태로 감쇠한다.
저탄소강과 같은 일부 재료는 변형 속도가 증가하면 항복 응력이 증가한다. 이 예에서 하중 속도가 높아서 변형률 속도 의존성이 중요할 가능성이 크다.
속도 의존성을 재료 정의에 추가한다.
속도 의존성을 금속 소성 재료 모델에 추가하려면 다음과 같이 설정한다.
1. 모델 트리에서 Materials 컨테이너 아래의 Steel을 두 번 클릭한다.
2. Edit Material 대화 상자의 재료 모델 목록에서 Plastic을 선택한다.
3. Suboptions → Rate dependent를 선택한다.
4. 표시된 Suboption Editor에서 Multiplier에 40을 입력하고, Exponent에 5를 입력하고 OK를 클릭한다.
이 속도 의존 거동의 정의에서 정적 항복 응력에 대한 동적 항복 응력의 비율(R)로부터 등가 소성 변형률 속도(ˉ˙εpl)가 식 ˉ˙εpl=D(R−1)n에 따라 얻어진다. 여기서 D와 n은 재료 상수이다. 이 예에서 40과 5이다.
단계 Blast의 시간 폭을 원래 값의 50 ms로 되돌린다. 작업 Blast_Load_Rate_Dep를 만들고 해석 작업을 제출한다. 해석이 완료되면 ODB 파일 Blast_Load_Rate_Dep.odb를 열고 결과를 후처리한다.
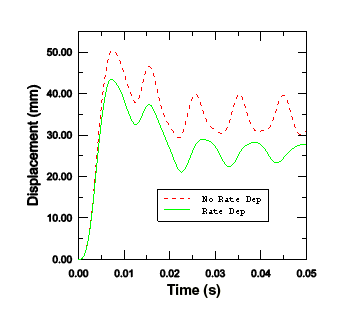
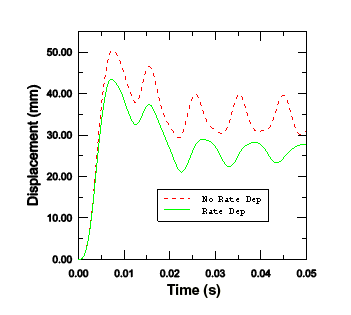
속도 의존성을 포함하면 변형률 속도가 증가하면 항복 응력도 증가한다. 따라서 탄성 계수는 소성 계수보다 크기 때문에 속도 의존성 해석은 응답이 단단해질 것으로 예상된다. 속도 의존성을 고려할 때, 반응이 실제로 단단해지는 것은 다음 그림에 표시된 플레이트의 중심 부분 변위의 시간 이력과 소성 변형률 에너지의 시간 이력 모두에서 확인할 수 있다. 당연히 이 결과는 재료 데이터에 민감하다. 이 예제에서, D와 n 의 값은 전형적인 저탄소강 값이다. 그러나 상세 설계 해석에는 더 정확한 데이터가 필요하다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 예제: 축대칭 마운트 (0) | 2024.06.01 |
|---|---|
| [Abaqus] 초탄성 해석이란? (1) | 2024.05.31 |
| [Abaqus] 예제: 소성을 고려한 연결용 러그 (0) | 2024.05.31 |
| [Abaqus] 탄소성 문제의 요소 선택 (0) | 2024.05.31 |
| [Abaqus] 연성 금속 재료의 소성 특성 (0) | 2024.05.31 |