고정 헤더 영역
상세 컨텐츠
본문
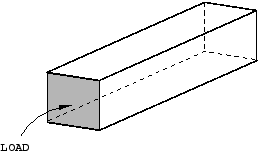
이 예제에서 이전에 ‘Abaqus 기초’에서 설명한 외연적 동역학의 몇 가지 기본 아이디어를 설명한다. 또한 안정 한계와 해석 시간에 대한 요소망 분할과 재료 특성의 영향을 설명한다. 이 막대는 다음 그림과 같다.
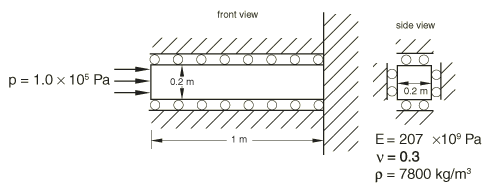
문제를 1차원 변형 문제로 만들기 위해 네 가지 측면 모두 롤러가 있다. 따라서 이 3차원 모델은 1차원 문제를 해석한다. 재료는 위 그림에 표시된 특성을 가진 강철이다. 막대의 자유 단은 1.0×105Pa의 크기와 3.88×10-5초의 지속 시간을 갖는 폭발 하중을 받는다. 정규화된 하중 크기는 다음 그림과 같다.
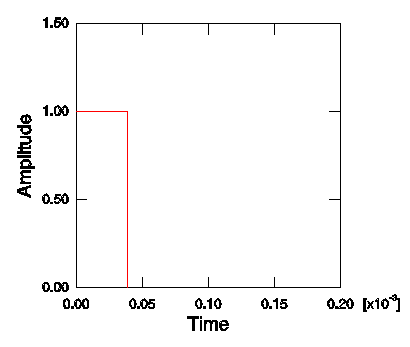
1) 전처리
이 예제는 Solid 돌출 기능으로 3차원 변형체를 만든다. 먼저 막대의 2차원 단면 형상을 스케치한 다음 단면 형상을 밀어낸다. 파트를 만들려면 다음과 같이 설정한다.
1. 새 파트 바를 만들고 Create Part 대화 상자에서 기본 설정인 3차원 변형체와 Solid 돌출 기본 기능을 그대로 사용한다. 0.5의 근사 크기를 모델에 사용한다.
2. 다음 그림에 표시된 치수를 사용하여 막대의 단면 모양을 스케치한다.
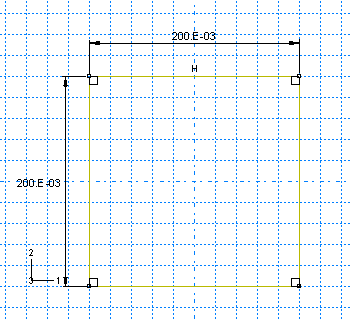
예를 들어, 다음 방법을 사용할 수 있다. Create Lines : Rectangle 도구를 사용하여 원점을 중심으로 사각형을 만든다. 단면이 높이 0.20m×너비 0.20m가 되도록 스케치에 치수를 입력한다. 단면 모양의 스케치가 완료되면 프롬프트에서 Done을 클릭한다. Edit Base Extrusion 대화 상자가 나타난다. 파트를 완성하려면 단면 모양을 밀어내는 거리를 입력해야 한다. 대화 상자에서 1.0m의 돌출 깊이를 입력한다.
⊙ 스케치 평면의 원점을 통과하는 수평과 수직 고정 구조선을 작성하고 적절한 형상 구속을 스케치에 제공한다.
3. 모델을 모델 데이터베이스 파일 Bar.cae에 저장한다.
질량 밀도가 7,800kg/m3, 영률이 207E9 Pa, 푸아송의 비가 0.3인 단일 선형 탄성 재료 Steel을 만든다. 재료를 Steel로 만든 solid, homogeneous 요소 특성 정의 Bar Section을 만든다. 요소 특성 정의 Bar Section을 전체 부분에 지정한다.
막대의 Instance 만든다. 이 모델은 기본적으로 전체 세 번째 축이 막대의 길이 방향이 되도록 방향이 지정된다.
다음 그림과 같이 형상 세트 TOP, BOT, FRONT, BACK, FIX, OUT을 만든다(세트 OUT에는 그림에 굵은 선으로 표시된 모서리가 포함된다). 그림과 같이 서피스 LOAD를 만든다. 나중에 이 영역은 하중과 경계 조건 적용과 출력 요청 정의에 사용된다.
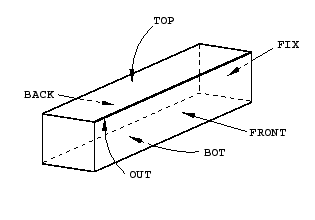
단일 동적 외연적 단계 Blast Load를 만든다. 단계 설명에 Apply pressure load pulse를 입력하고, 시간 폭을 2.0E-4초로 설정한다. Edit Step 대화 상자에서 Other 탭을 클릭한다. 가능한 한 응력파의 날카로움이 유지되도록 Quadratic bulk viscosity parameter를 ‘0’으로 설정한다.
단계 Blast Load의 경우 사전 선택된 필드 데이터가 출력 데이터베이스에 4개로 나눈 시간 간격으로 기록되도록 기본 필드 출력 요청을 편집한다.
기존 기본 이력 출력 요청을 삭제하고 새 이력 출력 요청을 만든다. Create History Output 대화 상자에서 기본 이름인 H-Output-1을 그대로 사용하고 Blast Load 단계를 선택한다. Continue를 클릭한다. Domain 필드 옆의 화살표를 클릭하고, Set을 선택하고 OUT을 선택한다. Output Variables 영역에서 Stresses의 왼쪽에 있는 삼각형을 클릭한다. S, Stress components and invariants 왼쪽에 있는 삼각형을 클릭하여 S33 변수를 켠다. 이것은 막대의 축 방향 응력 성분이다. 출력이 모든 증분에서 저장되도록 지정한다.
경계 조건 Fix right end를 작성하고 막대의 오른쪽 가장자리(기하 형상 세트 FIX)를 세 방향으로 구속한다. 추가 경계 조건을 작성하여 상단, 하단, 전면, 후면은 각 면의 법선 방향으로 구속한다(세트 FRONT와 BACK은 1방향, 세트 TOP과 BOT는 2방향).
폭발 하중은 최댓값으로 바로 적용되며 3.88×10-5초 동안 일정하게 유지된다. 그다음 하중은 바로 제거되고 ‘0’으로 유지된다. 다음 그림에 표시된 데이터를 사용하여 시간 변화 정의 Blast를 만든다. 이 예에서 주어진 시간의 압력 하중은 지정된 압력 하중의 크기에 시간 변화 곡선에서 보간(補間)한 값을 곱한 값이다.
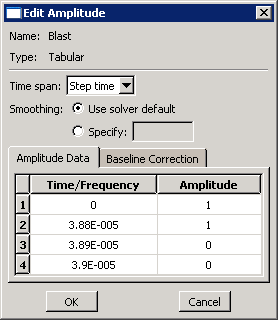
압력 하중 Blast load를 생성하고 하중이 적용되는 단계에서 Blast Load를 선택한다. 이 하중을 서피스 LOAD에 적용한다. 분포에 Uniform을 선택하고, 하중 크기에 1.0E5 Pa의 값을 지정하고, 시간 변화에 Blast를 선택한다.
재료 특성(푸아송의 비는 무시)을 사용하여 이전에 설명한 방정식을 사용하여 재료의 소밀파 속도를 계산할 수 있다.
$$ c_d = \sqrt{E \over \rho} = \sqrt{207 \times 10^9 Pa \over 7800 kg/m^3} = 5.15 \times 10^3 m/s $$
이 속도는 응력파가 1.94×10-4초로 막대의 고정단까지 도달한다. 시간이 지나면서 막대의 길이 방향으로 응력이 전파하는지 확인한다. 따라서 응력파가 정확하게 포착되는 충분히 미세한 요소망이 필요하다. 폭발 하중이 10개 요소의 길이에 걸쳐 발생한다고 가정한다. 이 10개 요소의 길이를 결정하려면 폭발 지속 시간에 소밀파 속도를 곱한다.
$$ L_{10el} = (3.88 \times 10^{-5} s)_{c_d} $$
10개 요소의 길이는 0.2m이다. 막대의 전체 길이는 1.0m이므로 길이 방향으로 50개의 요소를 제공한다. 요소망을 균일하게 하려면, 횡 방향으로 각각 10개의 요소를 주어, 50×10×10의 요소망을 작성한다. 이 요소망을 다음 그림에 나타낸다.
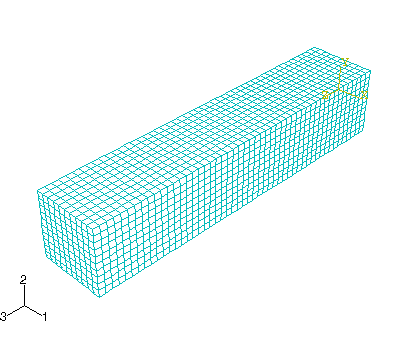
원하는 요소 크기가 0.02인 Seed를 전체 파트에 입력한다. Explicit 라이브러리에서 요소 종류로 C3D8R을 선택하고, 파트를 요소망으로 나눈다.
2) 해석
작업 Bar를 만들고 작업 설명에 Stress wave propagation in a bar(SI units)를 입력한다. 이 작업을 제출하고 결과를 관찰한다. 오류가 발생하면 모델을 수정하고, 해석을 다시 실행한다. 경고 메시지가 있으면 원인을 조사하고 적절히 조처한다. 앞에서 언급했듯이 일부 경고 메시지는 무시해도 괜찮지만 그렇지 않으면 수정 조치가 필요하다.
작업 진행 상황을 관찰하려면 상태 파일 Bar.sta를 볼 수도 있다. Job Monitor의 Status File 탭을 클릭하여 이 파일을 찾아보고 검색할 수 있다. 상태 파일은 관성 모멘트 정보를 출력한 다음 안정 한계 정보를 따른다. 가장 작은 안정 시간 한계를 갖는 10개의 요소가 순위별로 나열된다.
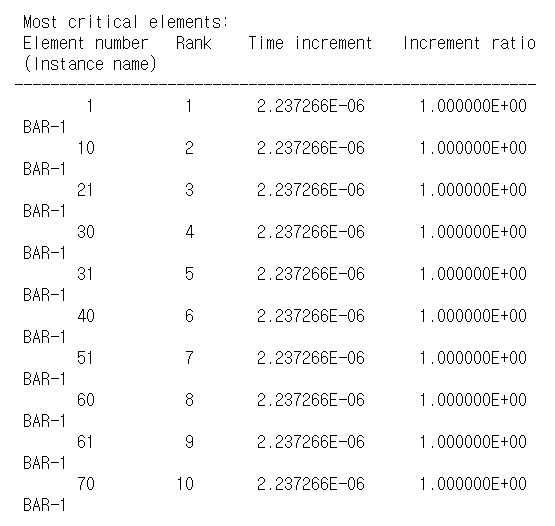
상태 파일에는 해석 진행 상황에 대한 정보가 계속 출력된다.
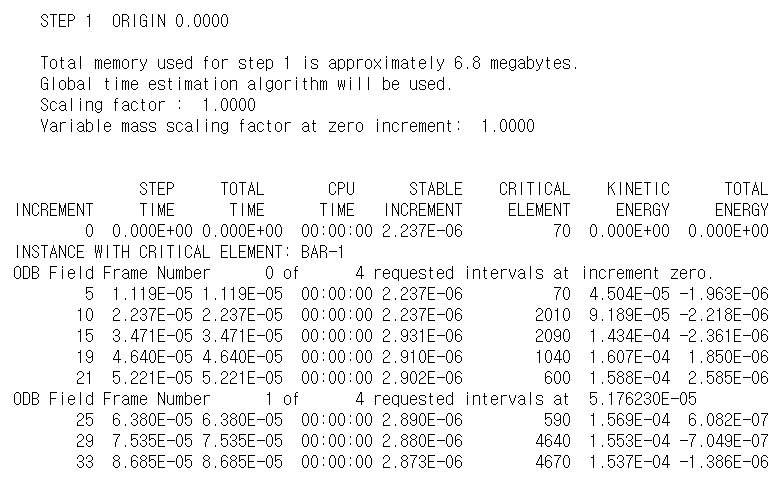
유사한 정보가 Visualization 모듈의 Job Diagnostics 대화 상자에 나타난다. 다음 그림과 같이 이 대화 상자에서 데이터의 시간 기록을 표시할 수 있다. 시간 기록 표시를 만들려면 Job History에서 단계를 선택하고 Incrementation 탭에서 열을 선택한 다음 Plot selected column을 클릭한다.
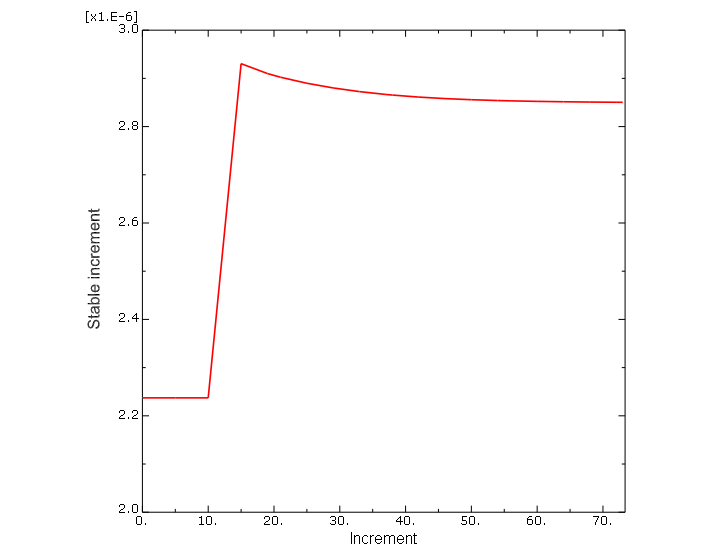
3) 후처리
모델 트리에서 작업 이름 Bar를 마우스 버튼 3으로 클릭하고 표시된 메뉴에서 Results를 선택하여 Visualization 모듈을 시작한다. 이때 이 작업에서 생성된 ODB 파일이 자동으로 열린다. 또는 Module 목록에서 Visualization 모듈을 시작한다. 기본 메뉴 막대에서 File → Open을 선택하고, 사용할 파일을 두 번 클릭하여 ODB 파일을 연다.
막대의 길이 방향을 따라 응력 분포가 시간에 따라 어떻게 변하는지 확인한다. 이를 위해 해석 과정에서 세 가지 다른 시간 동안 응력 분포를 살펴보자.
막대 축을 따라 세 번째 방향 응력(S33)의 변화를 나타내는 곡선을 ODB 파일의 처음 세 프레임에 대해 각각 만든다. 이 표시를 만들려면, 먼저 막대 축을 따라 직선 경로를 정의해야 한다.
막대의 중심을 따라 점 목록 경로를 만들려면 다음과 같이 설정한다.
1. 결과 트리에서 Paths를 두 번 클릭한다. Create Path 대화 상자가 나타난다.
2. 경로 이름을 Center로 지정한다. 경로 종류로 Point list를 선택하고 Continue를 클릭한다. Edit Point List Path 편집 대화 상자가 나타난다.
3. Point Coordinates 테이블에 바의 양쪽 끝에 중심 좌표를 입력한다. 이 입력은 모델의 글로벌 좌표계에 정의된 첫 번째 지점에서 두 번째 지점까지의 경로이다.
⊙ 앞의 절차를 사용하여 기하 형상과 요소망을 만들었다면 테이블 입력은 0, 0, 1과 0, 0, 0이다. 다른 절차를 사용하여 막대의 기하 형상을 만들면 Query 툴바의 도구를 사용하여 막대 가장자리의 중심 좌표를 결정할 수 있다.
4. 입력이 완료되면 OK를 클릭하여 Edit Point List Path 편집 대화 상자를 닫는다.
세 가지 다른 시간에 경로를 따라 응력 X-Y 표시를 저장하려면 다음과 같이 설정한다.
1. 결과 트리에서 XYData를 두 번 클릭한다. Create XY Data 대화 상자가 나타난다.
2. X-Y 데이터 소스에서 Path를 선택하고 Continue를 클릭한다. XY Data from Path 대화 상자가 나타나면 생성된 경로가 유효한 경로 목록에 표시된다. 원형 모델 모양이 표시되면 선택한 경로가 표시에서 강조 표시된다.
3. Point Locations 아래의 Include intersections를 선택한다.
4. 이 대화 상자의 X Values 영역에서 선택한 True distance를 그대로 사용한다.
5. 이 대화 상자의 Y Values 영역에서 Field Output을 클릭하여 Field Output 대화 상자를 연다.
6. S33 응력 성분을 선택하고 OK를 클릭한다.
XY Data from Path에서 경로 데이터 대화 상자의 필드 출력 변수가 변경되어 세 번째 방향의 응력 데이터(S33)가 생성됨을 나타낸다.
⊙ Abaqus/CAE는 필드 출력 변수가 현재 이미지에 표시되지 않음을 경고할 수 있다. 표시 상태를 As is로 설정하고 OK를 클릭하여 계속한다.
7. XY Data from Path 대화 상자의 Y Values 영역에서 Step/Frame을 클릭한다.
8. Step/Frame 대화 상자가 나타나면 프레임 1을 선택한다. 이것은 5개의 기록된 프레임 중 두 번째 프레임이다. (목록의 첫 번째 프레임인 프레임 0은 단계가 시작될 때 모델의 기준 상태이다) OK를 클릭한다. XY Data from Path에서 경로 값 대화 상자의 Y Values 영역이 변경되어 1단계의 프레임 1에서 데이터가 만들어진 것을 나타낸다.
9. X-Y 데이터를 저장하려면 Save As를 클릭한다. Save XY Data As 대화 상자가 나타난다.
10. X-Y 데이터의 이름을 S33_T1로 지정하고 OK를 클릭한다. S33_T1은 결과 트리의 XYData 컨테이너에 표시된다.
11. 7~9단계를 반복하여 프레임 2와 3에 대한 X-Y 데이터를 만든다. 이 데이터 세트의 이름은 각각 S33_T2과 S33_T3이다.
12. 경로에서 XY Data from Path 대화 상자를 닫고 Cancel을 클릭한다.
응력 곡선을 표시하려면 다음과 같이 설정한다.
1. XYData 컨테이너에서 커서를 드래그하여 세 개의 X-Y 데이터 세트를 모두 선택한다.
2. 마우스 버튼 3을 클릭하고 표시된 메뉴에서 Plot을 선택한다. 프레임 1, 2, 3에서 막대의 중심을 따라 세 번째 방향의 응력이 표시된다. 이 프레임은 약 5×10-5초, 1×10-4초, 1.5×10-4초의 해석 시간에 각각 해당한다.
3. 프롬프트에서 X을 클릭하여 현재 작업을 취소한다.
X–Y 표시를 사용자 정의하려면 다음과 같이 설정한다.
1. Y축을 두 번 클릭한다. Axis Options 대화 상자가 나타난다. Y Axis가 선택된다.
2. Scale 탭의 Tick Mode 영역에서 By increment를 선택하고 Y축의 주 눈금선이 20E3 Pa 간격으로 표시되도록 지정한다. 각 축의 제목도 사용자 정의할 수 있다.
3. Title 탭으로 전환한다.
4. Y축 제목에 Stress – S33 (Pa)을 입력한다.
5. X축을 편집하려면 대화 상자의 X Axis 필드에서 축 레이블을 선택한다. 대화 상자의 Title 탭에서 X 축 제목에 Distance along bar(m)을 입력한다.
6. Dismiss를 클릭하여 Axis Options 대화 상자를 닫는다.
X–Y 선도를 표시하는 방법을 사용자 정의하려면 다음과 같이 설정한다.
1. Visualization 도구 상자에서 아이콘을 클릭하여 Curve Options 대화 상자를 연다.
2. Curves 필드에서 S33_T2를 선택한다.
3. S33_T2 커브에 대해 점선 스타일을 선택한다. S33_T2 커브가 점선으로 표시된다.
4. 2단계와 3단계를 반복하여 S33_T3 커브를 점선으로 만든다.
5. Curve Options 대화 상자를 닫는다.
사용자 정의 표시는 다음 그림에 나와 있다(편의를 위해 기본 그리드와 범례의 위치가 변경되었다).
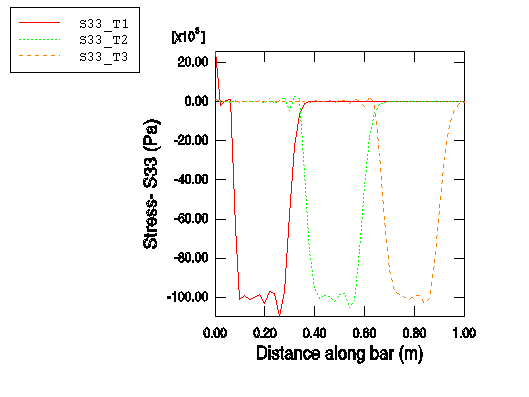
이 3개의 곡선 각각에서 응력파의 영향을 받는 막대의 길이는 약 0.2m임을 알 수 있다. 이 거리는 폭풍파가 적용 시간 동안 전달되는 거리와 일치해야 한다. 이것은 간단한 계산으로 확인할 수 있다. 파면의 길이가 0.2m이고, 파의 속도가 5.15×103m/s이면, 그 파가 0.2m 전해지는 데 걸리는 시간은 3.88×10-5초이다. 예상대로, 이것은 적용된 폭풍 하중의 지속 시간이다. 이 응력파는 막대의 축을 전달할 때 엄격한 4각형이 아니다. 특히, 응력이 급속히 변한 후에는 응력의 ‘링잉(ringing)’ 또는 진동이 발생한다. 선형 체적 점성은 이 링잉을 감쇠시켜 결과에 미치는 부정적인 영향을 방지한다.
결과를 조사하는 또 다른 방법은 막대의 세 가지 다른 지점에서 응력의 시간 기록을 표시하는 것이다. 예를 들어, 막대의 하중 가장자리에서 0.25m, 0.50m, 0.75m 떨어진 위치에서 볼 수 있다. 이렇게 하려면 먼저 이 위치에 있는 요소의 이름을 식별해야 한다. 이를 쉽게 수행하는 방법은 막대 가장자리를 따라 요소로 구성된 표시 그룹(세트 OUT)에서 요소를 Query하는 것이다.
요소 레이블을 Query하려면 다음과 같이 설정한다.
1. 결과 트리에서 ODB 파일 Bar.odb 아래에 있는 Element Sets 컨테이너를 확장한다. 세트 OUT을 마우스 버튼 3으로 클릭하고, 표시된 메뉴에서 Replace를 선택한다.
2. 기본 메뉴 모음에서 Tools → Query를 선택하거나 Query 툴바의 ⓘ 도구를 사용한다.
3. 나타나는 Query 대화 상자에서 Element를 클릭한다.
4. 다음 그림의 파란색 색상 요소를 클릭한다(바를 따라 13번째 요소). 요소 ID(레이블)가 프롬프트 및 메시지 영역에 표시된다. 세 가지 주황색 요소에 요소 레이블을 기록한다.
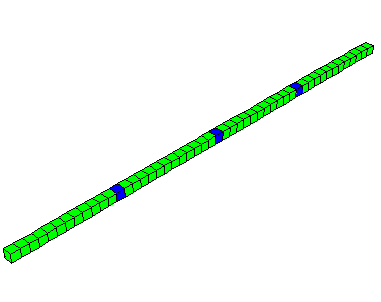
응력의 시간 기록을 표시하려면 다음과 같이 설정한다.
1. 결과 트리에서 History Output을 마우스 버튼 3으로 클릭하고 표시된 메뉴에서 Group Children을 선택 취소한다.
2. 3개의 특정 요소(13번째 요소)에 대한 데이터를 선택한다. [Ctrl]+클릭을 사용하여 여러 X–Y 데이터 세트를 선택한다.
3. 마우스 버튼 3을 클릭하고, 표시된 메뉴에서 Plot을 선택한다. 각 요소의 세로 응력 대 시간 X-Y 표시가 표시된다.
4. 프롬프트에서 X를 클릭하여 현재 작업을 취소한다.
이전과 마찬가지로 표시하는 방법을 사용자 정의할 수 있다.
X–Y 표시를 사용자 정의하려면 다음과 같이 설정한다.
1. X축을 두 번 클릭한다. Axis Options 대화 상자가 나타난다.
2. Title 탭으로 전환한다.
3. X축 제목에 Total time (s)을 지정한다.
4. Dismiss를 클릭하여 대화 상자를 닫는다.
X–Y 선도를 표시하는 방법을 사용자 정의하려면 다음과 같이 설정한다.
1. Visualization 도구 상자에서 아이콘을 클릭하여 Curve Options 대화 상자를 연다.
2. Curves 필드에서 막대의 자유 가장자리에 가장 가까운 요소에 해당하는 임시 X-Y 데이터 이름을 선택한다(이 세트의 요소 중에서 이 요소는 먼저 응력파의 영향을 받는다).
3. 곡선 범례 텍스트에 S33-0.25를 입력한다.
4. Curves 필드에서 막대 중앙의 요소에 해당하는 임시 X-Y 데이터 이름을 선택한다. (이것은 다음으로 응력파의 영향을 받는 요소이다.)
5. 곡선 범례 텍스트에 S33-0.5를 지정하고 곡선 스타일을 점선으로 변경한다.
6. Curves 필드에서 막대의 고정 가장자리에 가장 가까운 요소에 해당하는 임시 X-Y 데이터 레이블을 선택한다(이것은 마지막으로 응력파의 영향을 받는 요소이다).
7. 곡선 범례 텍스트에 S33-0.75를 지정하고 곡선 스타일을 파선으로 변경한다.
8. Dismiss를 클릭하여 대화 상자를 닫는다.
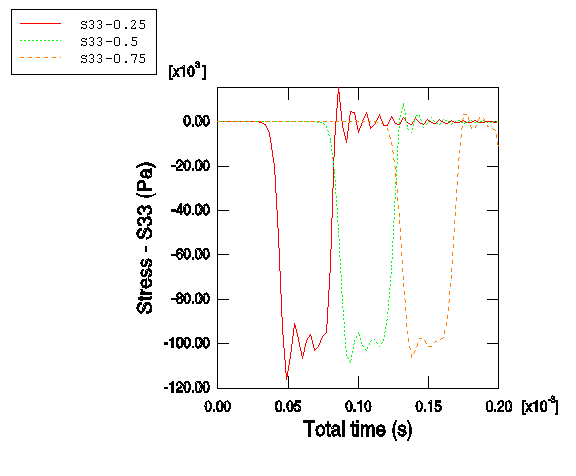
사용자 정의된 표시가 그림에 나와 있다(편의를 위해 기본 그리드와 범례의 위치가 변경되었다).
이 시간 기록 표시에서 각 지점에서 응력은 응력파가 그 지점을 통과할 때 증가하는 것을 알 수 있다. 응력파가 점을 완벽히 통과하면 점에서의 응력은 0을 중심으로 진동한다.
4) 요소망이 안정 시간 증분과 CPU 시간에 미치는 영향
‘자동 시간 증분 기능과 안정성’은 요소망의 미세한 정도가 안정 한계와 CPU 시간에 미치는 영향을 설명했다. 이 절은 파동 전파 문제에서 이 영향을 설명한다. 앞의 설명에서 길이 방향으로 50개의 요소를 가지며, 두 개의 가로 각각에 10개의 요소를 가진 잘 나눠진 6면체 요소의 요소망을 사용했다. 여기서 설명을 위해 25×5×5요소의 거친 요소망을 사용하고, 이 요소망을 다양한 방향으로 미세하게 나누면 CPU 시간이 무엇이 달라지는지 조사한다. 이 네 가지 요소망은 다음 그림과 같다.
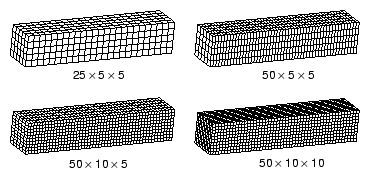
다음 표는 이 문제의 CPU 시간(거친 요소망 모델의 결과로 정규화된 값)이 요소망의 세부 사항에 따라 무엇이 달라지는지 보여준다. 이 표의 전반부는 이 책에 제시된 단순 안정성 방정식을 바탕으로 예측한 결과이다. 테이블의 뒷부분은 워크스테이션의 Abaqus/Explicit에서 이 해석을 수행하여 얻은 결과이다.
표. 요소망의 미세 정도와 해석 시간
| 요소망 | 단순화된 이론값 | 실제 값 | ||||
| $ \Delta t_{stable} $ (s) | 요소수 | CPU 시간(s) | 최대 $ \Delta t_{stable} $ (s) | 요소수 | 정규화된 CPU 시간 |
|
| 25×5×5 | A | B | C | 5.754E-06 | 625 | 1 |
| 50×5×5 | A/2 | 2B | 4C | 2.954E-06 | 1250 | 4 |
| 50×10×5 | A/2 | 4B | 8C | 2.933E-06 | 2500 | 8.33 |
| 50×10×10 | A/2 | 8B | 16C | 2.907E-06 | 5000 | 16.67 |
이론값의 결과에서 가장 거친 25×5×5 요소망을 기준 상태로 선택하고 안정 시간 증분, 요소 수와 CPU 시간을 각각 변수 A, B, C로 정의한다. 요소망을 세분화하면 최소 요소 치수가 감소하고, 요소망 요소 수가 증가한다. 이 효과는 각각 CPU 시간을 증가시킨다. 50×5×5 요소망에서 최소 요소 치수가 절반으로 감소하고, 요소 수가 2배가 되므로 CPU 시간은 원래 요소망의 4배로 증가한다. 하지만 요소망을 두 배로 나누어 50×10×5로 해도 최소 요소 치수는 변하지 않는다. 요소수가 2배가 될 뿐이다. 따라서 CPU 시간은 50×5×5 요소망의 두 배로 증가한다. 요소가 균일하고 50×10×10의 정사각형 요소망이 되도록 요소망을 나누면 요소 수와 CPU 시간이 다시 두 배가 된다.
이 단순 계산은 요소망 세분화가 안정 시간 증분과 CPU 시간에 미치는 영향의 경향을 매우 잘 예측한다. 하지만 안정 시간 증분의 예측값과 실제 값을 비교하지 않은 것은 몇 가지 이유가 있다. 첫째, 앞에서 설명한 것처럼 안정 시간 증분은 다음과 같이 계산한다.
$$ \Delta t_{stable} = {L^e \over c_d} $$
그리고 특성 요소 길이($ L^e $)는 최소 요소 치수라고 가정했다. 대조적으로 Abaqus/Explicit는 실제로 전체 요소의 크기와 모양을 바탕으로 특성 요소의 길이를 결정한다. 또한 문제를 복잡하게 만드는 요인으로 Abaqus/Explicit가 채택한 전반적인 안정 한계 추정이 있다. 이 추정은 더 큰 안정 시간 증분을 사용한다. 이런 요인이 있으므로 해석을 수행하기 전에 안정 시간 증분을 정확하게 예측하기는 어렵다. 그러나 추세는 단순 이론에 따른 것과 잘 일치하므로 안정 시간 증분이 요소망 세분화와 함께 어떻게 변하는지를 예측하는 것은 간단하다.
5) 재료가 안정 시간 증분과 CPU 시간에 미치는 영향
다른 재료에서 수행한 같은 파동의 전파 해석은 재료의 소밀파 속도에 따라 다른 CPU 시간이 걸린다. 예를 들어, 재료를 강철에서 알루미늄으로 바꾸면 소밀파 속도는 5.15×103m/s에서 다음으로 변경된다.
알루미늄에서 강철로 변하면 강성과 질량 밀도의 변화량이 거의 같으므로 안정 시간 증분에 미치는 영향은 적다. 납의 경우 이 차이가 더 크기 때문에 소밀파 속도는 다음으로 감소한다.
$$ c_d = \sqrt{E \over \rho} = \sqrt{14 \times 10^9 Pa \over 11240 kg/m^3} = 1.12 \times 10^3 m/s $$
이것은 강철 소밀파 속도의 약 1/5이다. 납의 안정 시간 증분은 강철 안정 시간 증분의 5배이다.
'공학 > 유한요소해석' 카테고리의 다른 글
| [Abaqus] 에너지 균형 (Abaqus/Explicit) (0) | 2024.05.31 |
|---|---|
| [Abaqus] 동적 진동 감쇠(Abaqus/Explicit) (0) | 2024.05.30 |
| [Abaqus] 자동 시간 증분 기능과 안정성 (0) | 2024.05.29 |
| [Abaqus] 외연적 동적 유한요소법 (0) | 2024.05.28 |
| [Abaqus] 비선형 외연적 동역학 해석 (0) | 2024.05.28 |





